Basic operations and concepts - math word problems - page 309 of 323
Number of problems found: 6445
- Covid-19
 Data showed that 22% of people in a small town were infected with the COVID-19 virus. A random sample of six residents from this town was selected. Find the probability that exactly two of these residents were infected.
Data showed that 22% of people in a small town were infected with the COVID-19 virus. A random sample of six residents from this town was selected. Find the probability that exactly two of these residents were infected. - Vinegar 2
 If we mix 3.5 liters of 5.8 % vinegar with 5 liters of 7.6 % vinegar, how many percentages of vinegar solution will we get?
If we mix 3.5 liters of 5.8 % vinegar with 5 liters of 7.6 % vinegar, how many percentages of vinegar solution will we get? - Alarm clock
 The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options.
The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options. - Mixture of nuts
 We should prepare the mixture of nuts from almonds, peanuts, and nuts cashew ratio of 1:2:3 (respectively). The price of almonds is 150 CZK/kg, the price of peanuts is 140 CZK/kg, and the price of cashew nuts is 180 CZK/kg. The price of the mixture is det
We should prepare the mixture of nuts from almonds, peanuts, and nuts cashew ratio of 1:2:3 (respectively). The price of almonds is 150 CZK/kg, the price of peanuts is 140 CZK/kg, and the price of cashew nuts is 180 CZK/kg. The price of the mixture is det - Six questions test
 There are six questions in the test. There are three answers to each - only one is correct. To take the exam, students must answer at least four questions correctly. Alan didn't learn, so he circled the answers only by guessing. What is the probability th
There are six questions in the test. There are three answers to each - only one is correct. To take the exam, students must answer at least four questions correctly. Alan didn't learn, so he circled the answers only by guessing. What is the probability th - Safe key locks
 We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All
We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All - Employee reduction probability
 Seven women and 3 men work in one office. According to the new regulation, reducing the number of employees by three is necessary. In a random sample of employees, what is the probability that they will be fired: a. One woman and two men b. At least one w
Seven women and 3 men work in one office. According to the new regulation, reducing the number of employees by three is necessary. In a random sample of employees, what is the probability that they will be fired: a. One woman and two men b. At least one w - Gorilla fruit supply
 At the Prague Zoo, they need to know how long the fruit will last for the gorillas. The stock in the warehouse would last the female Kamba for 25 days, the male Richard for 20 days, and the little Nura even for 40 days. How long will the supply last if ev
At the Prague Zoo, they need to know how long the fruit will last for the gorillas. The stock in the warehouse would last the female Kamba for 25 days, the male Richard for 20 days, and the little Nura even for 40 days. How long will the supply last if ev - Line ratio division
 Draw the line AB = 14 cm and divide it by the reduction angle in the ratio of 2:9.
Draw the line AB = 14 cm and divide it by the reduction angle in the ratio of 2:9. - Probability
 A man had 4 coins, some $2, some $1. The coins had a number on one side and a picture on the other. The man flipped them, and the sum of the numbers on the tops of the coins was 1. The probability of this happening was 1/8. What was the probability that i
A man had 4 coins, some $2, some $1. The coins had a number on one side and a picture on the other. The man flipped them, and the sum of the numbers on the tops of the coins was 1. The probability of this happening was 1/8. What was the probability that i - Alcohol 2
 Two types of alcohol, one 46% and second 64%, give 16 liters of 54% alcohol. How many liters of each type are in the mixture?
Two types of alcohol, one 46% and second 64%, give 16 liters of 54% alcohol. How many liters of each type are in the mixture? - Four pavers
 Four pavers would pave the square in 18 days. How many pavers do you need to add to the done work in 12 days?
Four pavers would pave the square in 18 days. How many pavers do you need to add to the done work in 12 days? - Three-day trip
 George went on a moped for a three-day trip. He drove 90 km on the first day, 30 km on the second day, and 60 km on the third day. He always drove at the same average speed and always the whole number of hours. Calculate the average speed if George drove
George went on a moped for a three-day trip. He drove 90 km on the first day, 30 km on the second day, and 60 km on the third day. He always drove at the same average speed and always the whole number of hours. Calculate the average speed if George drove - Water current
 John swims upstream. After a while, he passes the bottle, and from that moment, he floats for 20 minutes in the same direction. He then turns around and swims back, and from the first meeting with the bottle, he sails 2 kilometers before he reaches the bo
John swims upstream. After a while, he passes the bottle, and from that moment, he floats for 20 minutes in the same direction. He then turns around and swims back, and from the first meeting with the bottle, he sails 2 kilometers before he reaches the bo - The shooter
 The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stops firing. (a) What is the most likely nu
The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stops firing. (a) What is the most likely nu - Boys and girls
 There are 11 boys and 18 girls in the classroom. Three pupils will answer. What is the probability that two boys will be among them?
There are 11 boys and 18 girls in the classroom. Three pupils will answer. What is the probability that two boys will be among them? - A ship
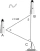 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Probability - tickets
 What is the probability when you have 25 tickets in 5000 that you do not win the first (one) prize?
What is the probability when you have 25 tickets in 5000 that you do not win the first (one) prize? - Two cities
 The car goes from city A to city B at an average speed of 70 km/h and back at an average speed of 50 km/h. If it goes to B and back at an average speed of 60 km/h, the whole ride will take 8 minutes less. What is the distance between cities A and B?
The car goes from city A to city B at an average speed of 70 km/h and back at an average speed of 50 km/h. If it goes to B and back at an average speed of 60 km/h, the whole ride will take 8 minutes less. What is the distance between cities A and B? - Exam pass probability
 During the exam, each student receives 30 different questions, from which he chooses 3 at random. To pass the exam, he needs to be able to answer two correctly. What is the probability that a student will pass if he mastered 70% of the questions (70% of t
During the exam, each student receives 30 different questions, from which he chooses 3 at random. To pass the exam, he needs to be able to answer two correctly. What is the probability that a student will pass if he mastered 70% of the questions (70% of t
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
