Complex numbers - practice problems - last page
Instructions: Solve each problem carefully and provide a detailed solution for every item.Number of problems found: 59
- Goniometric form
Determine the goniometric form of a complex number z = √ 110 +4 i. - The modulus
Find the modulus of the complex number 2 + 5i - In the shipment
There are 40 products in the shipment. Of these, 4 are defective. In how many ways can we select 5 products so that exactly 3 of them are good? - Moivre 2
Find the cube roots of 125(cos 288° + i sin 288°). - Alternating circuit
In an alternating circuit, the total voltage V is given by V=V1 +V2 If V=(12.2+6.8i) V and V1=(7.8-2.5i) V, find the voltage V2. - Root sum
What is the sum of the fifth root of 243? - Third roots
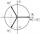Determine the sum of the three complex third roots of the number 64 . - Modulus and argument
Find the mod z and argument z if z=i - Complex square roots
Determine the sum of the three square roots of 343. - Complex roots Find the sum of the fourth square root of the number 16.
- Calculate roots of z
Calculate the ratio of the two fifth roots of the number 32. - Stadium
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter. - Distance two imaginary numbs Find the distance between two complex numbers: z1=(-8+i) and z2=(-1+i).
- Subtracting complex in polar
Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form? - ABS CN
Calculate the absolute value of the complex number -6+19i. - De Moivre's formula There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers.
- Cis notation Evaluate the multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation.
- ABS, ARG, CONJ, RECIPROCAL
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - Dipole - complex power
For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
