Geometry - math word problems - page 150 of 162
Number of problems found: 3232
- Brass sphere
Find the weight of a brass ball with an outer radius of 12 cm and a wall thickness of 20 mm if the brass's density is 8.5 g/cm³. - Cylinder-shaped part
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - Truncated pyramid
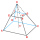Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm. - Candles
Before Christmas, Eva bought two cylindrical candles—red and green. Red was 1 cm longer than green. She lit a red candle on Christmas Day at 5:30 PM and a green candle at 7:00 PM, leaving them on fire until they burned. At 9:30 PM, both candles were the s - Reduction 33021
Draw the line AB = 14 cm and divide it by the reduction angle in the ratio of 2:9. - Hypotenuse 4221
Find the set of points formed by the center of gravity of right triangles with the same hypotenuse (build several possible triangles into one image). - Prescribed 4579
The racing ball for men has a prescribed weight of 7250g. It is made of iron. How does its diameter change if we make it from lead? The density of iron is 7.8 g / cm cubic, and the density of lead is 11.3 t / m cubic. - Square ABCD
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4]. - Identical 8831
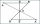In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P - Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - Hexagon = 8 parts
Divide the regular hexagon into eight equal parts. - Semicircles
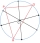In a rectangle with sides of 4cm and 8cm, there are two different semicircles, each of which has its endpoints at its adjacent vertices and touches the opposite side. Construct a square such that its two vertices lie on one semicircle, the remaining two o - Projection 3493
In axonometry, construct a projection of an oblique circular cone with a base in a plane. The stop triangle gives dimension. We know the center of the base S, the radius of the base ra the top of the cone V, Triangle (6,7,6), S (2,0,4), V (-2,7,6), r = 3 - GP - edge lengths
The block edge lengths are made up of three consecutive GP members. The sum of the lengths of all edges is 84 cm, and the volume block is 64 cm³. Determine the surface of the block. - Megapascals
What is the area of cross-section of the piston if the force of 300 kN produces a pressure of 5 MPa? - Measuring cork
Simon boasted that he had taken away a block of cork measuring 0.5m x 0.5m x 1.2m. Is it possible we know that 1 m of cubic cork weighs 300 kg and children from 10 to 15 years old can carry a maximum load of 5 kg? - Lines
How many points will intersect 27 different lines where no two are parallel? - Truncated 43851
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6m. Calculate how much m³ of soil was removed when we dug this pit. - Divides 70604
Draw a point x on the line, which divides it in the given ratio: a) 2:3 b) 1:5 c) 6:2 - Intersections 26781
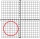A rectangular grid consists of two mutually perpendicular systems of parallel lines with a distance of 2. We throw a circle with a diameter of 1 on this plane. Calculate the probability that this circle: a) overlaps one of the straight lines; b) do any of
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
