Planimetrics - math word problems - page 181 of 185
Number of problems found: 3686
- Clouds
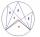 We see the cloud under an angle of 26°10' and the Sun at an angle of 29°15'. The shade of the cloud is 92 meters away from us. Approximately at what height is the cloud?
We see the cloud under an angle of 26°10' and the Sun at an angle of 29°15'. The shade of the cloud is 92 meters away from us. Approximately at what height is the cloud? - Function x*tanx
 Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph.
Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph. - Decide 2
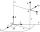 Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line
Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line - Cosine
 Calculate the cosine of the smallest internal angle in a right-angled triangle with cathetus 3 and 8 and the hypotenuse 8.544.
Calculate the cosine of the smallest internal angle in a right-angled triangle with cathetus 3 and 8 and the hypotenuse 8.544. - Right
 Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 2a +5b = 5.283c
Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 2a +5b = 5.283c - Depth angles
 At the top of the mountain stands a castle with a tower 30 meters high. We see the crossroad at a depth angle of 32°50' and the heel at 30°10' from the top of the tower. How high is the top of the mountain above the crossroad?
At the top of the mountain stands a castle with a tower 30 meters high. We see the crossroad at a depth angle of 32°50' and the heel at 30°10' from the top of the tower. How high is the top of the mountain above the crossroad? - Four sides of trapezoid
 In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles.
In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles. - Fighter
 A military fighter flies at an altitude of 10 km. The ground position was aimed at an altitude angle of 23° and 12 seconds later at an altitude angle of 27°. Calculate the speed of the fighter in km/h.
A military fighter flies at an altitude of 10 km. The ground position was aimed at an altitude angle of 23° and 12 seconds later at an altitude angle of 27°. Calculate the speed of the fighter in km/h. - Rhombus 48
 A rhombus consists of four identical rhombuses with an area of 42 m². The angle alpha of each rhombus is 60°. What is its perimeter?
A rhombus consists of four identical rhombuses with an area of 42 m². The angle alpha of each rhombus is 60°. What is its perimeter? - Angle of inclination
 What percentage of the gradient should be indicated on the mark if the angle of inclination of the road is 6°25'?
What percentage of the gradient should be indicated on the mark if the angle of inclination of the road is 6°25'? - Lift
 The largest angle at which the lift rises is 16°31'. Give climb angle in permille.
The largest angle at which the lift rises is 16°31'. Give climb angle in permille. - Wheel gear
 A drive wheel of radius two is connected to a drive wheel of radius one by a pulley of length 17. What is the distance between the wheel axles?
A drive wheel of radius two is connected to a drive wheel of radius one by a pulley of length 17. What is the distance between the wheel axles? - Right triangle eq2
 Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70. - Perimeter - ASA theorem
 Calculate the perimeter of the triangle ABC if a = 12 cm, the angle beta is 38 degrees, and the gamma is 92 degrees.
Calculate the perimeter of the triangle ABC if a = 12 cm, the angle beta is 38 degrees, and the gamma is 92 degrees. - Triangle area and angle
 Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the vertex A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 .
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the vertex A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 . - Ratio iso triangle
 The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures.
The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures. - Trapezoid 25
 Trapezoid PART with AR||PT has (angle P=x) and (angle A=2x) . In addition, PA = AR = RT = s. Find the length of the median of Trapezoid PART in terms of s.
Trapezoid PART with AR||PT has (angle P=x) and (angle A=2x) . In addition, PA = AR = RT = s. Find the length of the median of Trapezoid PART in terms of s. - Climb of the road
 At what angle does the road rise if the climb is 8%? They rounded up for tens of minutes.
At what angle does the road rise if the climb is 8%? They rounded up for tens of minutes. - Dipole - complex power
 For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice.
For a dipole, calculate the complex apparent power S and the instantaneous value of the current i(t), given: R=10 Ω, C=100uF, f=50 Hz, u(t)= square root of 2 * sin( ωt - 30°). Thanks for any help or advice. - Triangle in circle
 The vertices of the triangle ABC lie on a circle with a radius 3, which is divided into three parts in the ratio 4:4:4. Calculate the circumference of the triangle ABC.
The vertices of the triangle ABC lie on a circle with a radius 3, which is divided into three parts in the ratio 4:4:4. Calculate the circumference of the triangle ABC.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
