Planimetrics - math word problems - page 180 of 185
Number of problems found: 3686
- Two forces
 Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer.
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer. - Rhombus
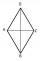 ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus.
ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus. - Calculate roots of z
 Calculate the ratio of the two fifth roots of the number 32.
Calculate the ratio of the two fifth roots of the number 32. - Railway
 The railway line had a 5.8 km segment climb nine permille. How many meters does the track ascent?
The railway line had a 5.8 km segment climb nine permille. How many meters does the track ascent? - Standing 22821
 The heating plant sees the observer standing 26 m from the bottom of the chimney and seeing the top at an angle of 67 °. Thus, the chimney of the heating plant is how high?
The heating plant sees the observer standing 26 m from the bottom of the chimney and seeing the top at an angle of 67 °. Thus, the chimney of the heating plant is how high? - Trapezoid MO
 The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid.
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Triangle - many properties
 In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - River
 From the observatory 18 m high and 31 m from the riverbank, river width appears in the visual angle φ = 20°. Calculate the width of the river.
From the observatory 18 m high and 31 m from the riverbank, river width appears in the visual angle φ = 20°. Calculate the width of the river. - Angle between vectors
 Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21)
Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21) - Calculate
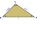 Calculate the area of triangle ABC if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm.
Calculate the area of triangle ABC if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm. - Chord 24
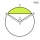 A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Slope
 What is the slope of a line with an inclination -325°?
What is the slope of a line with an inclination -325°? - Geodesist
 Triangle-shaped field (triangle ABC) has a side AB = 129 m. path XY is parallel to the side AB, which divides triangle ABC into two parts with the same area. What will be the length of path XY? Help, please, geodesist.
Triangle-shaped field (triangle ABC) has a side AB = 129 m. path XY is parallel to the side AB, which divides triangle ABC into two parts with the same area. What will be the length of path XY? Help, please, geodesist. - Height difference
 What height difference is overcome if we pass a road 1 km long with a pitch of 21 per mille?
What height difference is overcome if we pass a road 1 km long with a pitch of 21 per mille? - Road
 Between cities, A and B is a route 9 km long of average 9‰ klesanie. Calculate the height difference between cities A and B.
Between cities, A and B is a route 9 km long of average 9‰ klesanie. Calculate the height difference between cities A and B. - The tower
 The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands?
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands? - Three vertices
 The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A.
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Cablecar
 Funicular on Petrin (Prague) was 408 meters long and overcame the difference of 106 meters in altitude. Calculate the angle of the climb.
Funicular on Petrin (Prague) was 408 meters long and overcame the difference of 106 meters in altitude. Calculate the angle of the climb. - Traffic sign
 There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls).
There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls). - Altitude difference
 Between the resorts is 15 km, and the climb is 13 permille. What is the height difference?
Between the resorts is 15 km, and the climb is 13 permille. What is the height difference?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
