Planimetrics - math word problems - page 82 of 185
Number of problems found: 3683
- Rhombus 47
A rhombus has a side length of 5 m and a longer diagonal length of 8 m. What is the length of the shorter diagonal of the rhombus? - Square room 2
A square room has a floor area of 144 square feet. The height of the room is 6 feet. What is the area of one wall? - The length 13
The length of a rectangular garden is 3 5/11. The width is 1/4 of the length. What is the area of the garden as a mixed number? - A piece 3
A piece of rectangle cloth has an area of 2 4/5 meters. Its breadth is 1 1/5 meters. What is the length of the cloth? - ABC isosceles
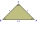ABC isosceles rights triangle the length of each leg is 1 unit what is the length of the hypotenuse AB in the exact form - The equator
Calculate the length of the equator. Calculate a radius of 6378 km. Round to the nearest thousand. - Procedure and calculation - Circumference - trapezoid
Calculate the circumference of the trapezoid if the lengths of the sides are as follows: a = 26 cm, b = square root of 50, c = 9 cm, d = 13 cm. - Rounding
What width and length in centimeters may have rectangle land when round the dimensions to the meter, the width is 5 m and length 7 meters? - Bicycle wheel
The bicycle wheel diameter is 62 cm. How many times turns the bicycle on the road 1 km long? - Triangle radians
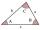The size of two internal angles of a triangle ABC is α=6/18π and β=7/18π. Calculate the size of the third angle. - Parallelogram
Calculate the area and perimeter of a parallelogram whose two sides are long a=18 cm b=14 cm and height ha = 2 cm long. - Hexagon
Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter? - Rhombus
Find the length of the other diagonal and the area of the rhombus. The perimeter of a rhombus is 56 cm, and one of the diagonals is of length 14 cm. - Right triangle
Right triangle ABC with side a = 10 and the area S = 50. Calculate the length of the remaining sides. - Circumscription
Calculate the radius of the Circumscribed circle in the rectangle with sides 3 and 6. Can it be a rectangle inscribed by a circle? - Triangle ABC
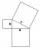Right triangle ABC with right angle at the C, |BC|=19, |AB|=26. Calculate the height of the triangle hAB to the side AB. - Square and circles
Square with sides 68 km is circumscribed and inscribed with circles. Determine the radiuses of both circles. - Described 83448
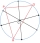A square is described as a circle with a radius of 6 cm. How much larger is the area of the square than the area of the circle? - The length 5
The length and breadth of a rectangular field are 3 1/5 m and 1 3/7 m. Find the area of the rectangular field. - A rectangle 6 A rectangle measures 2 4/5 inches by 2 1/5 inches. What is its area?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
