Planimetrics - math word problems - page 87 of 185
Number of problems found: 3686
- PT - Pythagorean
 A right triangle ABC has hypotenuse c and legs a, and b of the following lengths. Estimate the length of its remaining side and compare your estimates with your calculations. a) a = 4 cm; b = 5 cm b) a = 6.8 m; b = 9 m c) a= 8.9 m; b = 1 m d) b= 10 cm; c
A right triangle ABC has hypotenuse c and legs a, and b of the following lengths. Estimate the length of its remaining side and compare your estimates with your calculations. a) a = 4 cm; b = 5 cm b) a = 6.8 m; b = 9 m c) a= 8.9 m; b = 1 m d) b= 10 cm; c - Right triangle generator
 Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator?
Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator? - Triangular pyramid
 A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm.
A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm. - Circumference 66134
 The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid.
The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid. - Exchanged 4627
 Mr. Sova had a plot of land with an area of 3600 m². However, he exchanged it for another square plot, which was 5 m larger. How many m² does the larger land now have?
Mr. Sova had a plot of land with an area of 3600 m². However, he exchanged it for another square plot, which was 5 m larger. How many m² does the larger land now have? - Infinite sum of areas
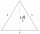 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Infinity
 A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares.
A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares. - Hypotenuses 83154
 In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Intersections 68784
 The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places.
The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places. - Five circles
 On the line segment CD = 6, there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE.
On the line segment CD = 6, there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE. - Extending square garden
 Mrs. Petrová's garden had a square shape with a side length of 15 m. After its enlargement by 64 m² (square), it became a square again. How many meters has the length of each side of the garden been extended?
Mrs. Petrová's garden had a square shape with a side length of 15 m. After its enlargement by 64 m² (square), it became a square again. How many meters has the length of each side of the garden been extended? - Triangle KLM
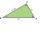 In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm.
In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm. - Tiles
 From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles.
From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles. - Recursion squares
 In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - Distance 79874
 The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed?
The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed? - IS trapezoid
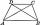 Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Ladder
 How long is a ladder that touches a wall 4 meters high and has a lower part 3 meters away from the wall?
How long is a ladder that touches a wall 4 meters high and has a lower part 3 meters away from the wall? - Face of the house
 How tall is the roof of a house in the shape of an isosceles triangle with a base length of 8 meters and an arm 5 meters long?
How tall is the roof of a house in the shape of an isosceles triangle with a base length of 8 meters and an arm 5 meters long? - Broken tree
 The tree was 35 meters high. The tree broke at a height of 10 m above the ground. Top, but does not fall off. It is refuted on the ground. How far from the base of the tree lay its peak?
The tree was 35 meters high. The tree broke at a height of 10 m above the ground. Top, but does not fall off. It is refuted on the ground. How far from the base of the tree lay its peak? - Triangle ABC
 Calculate the sides of the triangle ABC with an area of 725 cm², and if sides are in a ratio a: b: c = 9:19:11
Calculate the sides of the triangle ABC with an area of 725 cm², and if sides are in a ratio a: b: c = 9:19:11
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
