The Law of Cosines - practice problems - page 2 of 5
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 84
- The angle of view
 Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other.
Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other. - Diagonals
 Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°.
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°. - SAS calculation
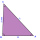 Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle α is 47°, find side a. Please round to one decimal.
Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle α is 47°, find side a. Please round to one decimal. - Largest angle of the triangle
 Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a
Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a - Diagonals in diamond
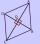 In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals.
In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals. - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - Parallelogram - angle alfa
 In the parallelogram ABCD the length of sides are AB = 8, BC = 5, BD = 7. Calculate the magnitude of the angle α = ∠DAB (in degrees).
In the parallelogram ABCD the length of sides are AB = 8, BC = 5, BD = 7. Calculate the magnitude of the angle α = ∠DAB (in degrees). - The farmer
 The farmer sees the back fence of the land, which is 50 m long at a viewing angle of 30 degrees. It is 92 m away from one end of the fence. How far is it from the other end of the fence?
The farmer sees the back fence of the land, which is 50 m long at a viewing angle of 30 degrees. It is 92 m away from one end of the fence. How far is it from the other end of the fence? - Triangle sides to angles
 The triangle ABC has side lengths a = 14 cm, b = 20 cm, c = 7.5 cm. Find the sizes of the angles and the area of this triangle.
The triangle ABC has side lengths a = 14 cm, b = 20 cm, c = 7.5 cm. Find the sizes of the angles and the area of this triangle. - ABCD
 AC= 40cm , angle DAB=38 , angle DCB=58 , angle DBC=90 , DB is perpendicular on AC , find BD and AD
AC= 40cm , angle DAB=38 , angle DCB=58 , angle DBC=90 , DB is perpendicular on AC , find BD and AD - Triangle from median
 Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5. - Four sides of trapezoid
 In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles.
In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles. - Rhombus - diagonals
 Rhombus ABCD has side a = 80 cm and side b = 50 cm. Diagonals u1 and u2 make an angle of 60 degrees with each other. Calculate the area of the rhombus.
Rhombus ABCD has side a = 80 cm and side b = 50 cm. Diagonals u1 and u2 make an angle of 60 degrees with each other. Calculate the area of the rhombus. - Heptagon perimeter
 Calculate a regular heptagon's perimeter if its shortest diagonal length is u=14.5cm.
Calculate a regular heptagon's perimeter if its shortest diagonal length is u=14.5cm. - Observation angle
 At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end?
At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end? - Children playground
 The playground has a trapezoid shape, and the parallel sides have a length of 36 m and 21 m. The remaining two sides are 14 m long and 16 m long. Find the size of the inner trapezoid angles.
The playground has a trapezoid shape, and the parallel sides have a length of 36 m and 21 m. The remaining two sides are 14 m long and 16 m long. Find the size of the inner trapezoid angles. - Measurements of a triangle
 Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft - Isosceles 7929
 ABCD isosceles trapezoid. A = 6cm, e = 7cm and delta angle = 105 °. Calculate the remaining pages.
ABCD isosceles trapezoid. A = 6cm, e = 7cm and delta angle = 105 °. Calculate the remaining pages. - On a mass
 The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make.
The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make. - Circumscribed circle
 In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle.
In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
