Triangle practice problems - page 112 of 125
Number of problems found: 2500
- Five circles
 On the line segment CD = 6, there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE.
On the line segment CD = 6, there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE. - Calculate 6214
 The cube A B C D A'B'C'D 'has a section area ACC'A' equal to 64 square root of 2 cm². Calculate the surface of the cube.
The cube A B C D A'B'C'D 'has a section area ACC'A' equal to 64 square root of 2 cm². Calculate the surface of the cube. - Tetrahedron 46451
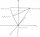 Calculate the surface of a regular tetrahedron if the length of the wall height v = 1 dm.
Calculate the surface of a regular tetrahedron if the length of the wall height v = 1 dm. - Quadrilateral ABCD
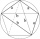 Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125° - Hexagonal pyramid
 Find the volume of a regular hexagonal pyramid, the base edge 12 cm long and the side edge 20 cm.
Find the volume of a regular hexagonal pyramid, the base edge 12 cm long and the side edge 20 cm. - Regular hexagonal pyramid
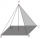 Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture.
Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture. - Pentagon
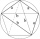 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Respectively 81293
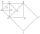 The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help...
The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help... - Calculate 8326
 Calculate the cone shell with a base diameter of 40 cm and a cone height of 50 cm.
Calculate the cone shell with a base diameter of 40 cm and a cone height of 50 cm. - Medians in triangle
 The median of the isosceles triangle is 3 cm long. If its perimeter is 16 cm, determine the size of its sides.
The median of the isosceles triangle is 3 cm long. If its perimeter is 16 cm, determine the size of its sides. - Body diagonal
 Cuboid with base 7cm x 3,9cm and body diagonal 9cm long. Find the height of the cuboid and the length of the diagonal of the base,
Cuboid with base 7cm x 3,9cm and body diagonal 9cm long. Find the height of the cuboid and the length of the diagonal of the base, - Parallelogram ABCD
 We have the parallelogram ABCD, where AB is 6.2 cm; BC is 5.4 cm and AC is 4.8 cm. Calculate the height on the AB side and the angle DAB.
We have the parallelogram ABCD, where AB is 6.2 cm; BC is 5.4 cm and AC is 4.8 cm. Calculate the height on the AB side and the angle DAB. - Same area
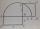 There is a given triangle. Construct a square of the same area.
There is a given triangle. Construct a square of the same area. - Distance
 Calculate the distance between two points K[6; -9] and G[5; -1].
Calculate the distance between two points K[6; -9] and G[5; -1]. - Prism
 A right prism's length, width, and height are 17, 11, and 11, respectively. What is the length of the longest segment whose endpoints are vertices of the prism?
A right prism's length, width, and height are 17, 11, and 11, respectively. What is the length of the longest segment whose endpoints are vertices of the prism? - Tower
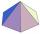 The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste.
The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste. - Quadrilateral pyramid
 The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Secret treasure
 Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure.
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure. - Hexa prism
 Determine the volume of the hex prism with a 4 cm edge base and a 28 cm body height.
Determine the volume of the hex prism with a 4 cm edge base and a 28 cm body height. - Quadrilateral 29201
 How much sheet is needed for a roof with the shape of a regular quadrilateral pyramid if its edge is 2.8 m long and the height of the roof is 0.8 m? Calculate 10% for the overlap (extra).
How much sheet is needed for a roof with the shape of a regular quadrilateral pyramid if its edge is 2.8 m long and the height of the roof is 0.8 m? Calculate 10% for the overlap (extra).
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
