Príklady pre 9. ročník (pre deviatakov) - strana 2 z 364
Deviatak by mal ovládať riešenie kvadratických rovníc (vzorec, rozklad, dopĺňanie na štvorec) a prácu s algebrickými výrazmi.Mal by zvládať geometriu – výpočty objemov a povrchov hranatých aj guľatých telies (valec, kužeľ, guľa) a aplikáciu Pytagorovej vety.
Nepostrádateľná je znalosť trigonometrie – sínus, kosínus, tangens v pravouhlom trojuholníku a riešenie praktických úloh (výška stromu, uhol sklonu).
Dôležité je pochopenie funkcií – lineárnych, kvadratických a ich grafov, vrátane práce so sústavou súradníc.
Mali by vedieť aplikovať percentá a úrokovanie v reálnych situáciách (pôžičky, zľavy) a základy štatistiky (priemer, grafické znázornenie dát).
Počet nájdených príkladov: 7277
- Školský klub ŠKD
 30 deti v školskom klube sa potrebuje rozdeliť do dvoch družstiev. Do košíka dali 15 bielych a 15 čiernych gulôčok a žrebujú. Družstvá budú tvotiť deti, ktoré si vytiahnu gulôčky rovnakej farby. Prvá ťahala Paťa a vytiahla bielu gulôčku. Po nej ťahá Marti
30 deti v školskom klube sa potrebuje rozdeliť do dvoch družstiev. Do košíka dali 15 bielych a 15 čiernych gulôčok a žrebujú. Družstvá budú tvotiť deti, ktoré si vytiahnu gulôčky rovnakej farby. Prvá ťahala Paťa a vytiahla bielu gulôčku. Po nej ťahá Marti - 216 povrch aj objem
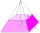 Vypočítaj povrch a objem pravidelného štvorbokého ihlana: a = 6 cm a telesová výška je 12 cm.
Vypočítaj povrch a objem pravidelného štvorbokého ihlana: a = 6 cm a telesová výška je 12 cm. - Rýdze zlato
 Koľko rýdzeho zlata obsahuje 15-gramový prsteň vyrobený zo 14-karátového zlata? Výsledok zaokrúhlite na desatiny gramu.
Koľko rýdzeho zlata obsahuje 15-gramový prsteň vyrobený zo 14-karátového zlata? Výsledok zaokrúhlite na desatiny gramu. - Zmenka predaj
 Podnikateľ kúpil zmenku 6 mesiacov pred lehotou splatnosti. Po odčítaní úroku pri úrokovej miere 10% p. a. zaplatil za ňu 19 000 €. Koľko € úroku sa odčítalo z nominalnej hodnoty zmenky?
Podnikateľ kúpil zmenku 6 mesiacov pred lehotou splatnosti. Po odčítaní úroku pri úrokovej miere 10% p. a. zaplatil za ňu 19 000 €. Koľko € úroku sa odčítalo z nominalnej hodnoty zmenky? - Traktor 19
 Traktor zorie lán poľa za 48 hodín s použitím pluhu so 5 radlicami. Ako dlho mu bude trvať orba toho istého poľa s pluhom so 6 rovnako širokými radlicami pri nezmenenej rýchlosti traktora?
Traktor zorie lán poľa za 48 hodín s použitím pluhu so 5 radlicami. Ako dlho mu bude trvať orba toho istého poľa s pluhom so 6 rovnako širokými radlicami pri nezmenenej rýchlosti traktora? - Natretie stĺpa
 Koľko kg farby potrebujeme na natretie stĺpa tvaru pravidelného trojbokého hranola s hranou podstavy dlhou 2,5 m a výškou na hranu podstavy 2 m, ak 1 kg farby vystačí na 25 m² náteru? Stĺp je vysoký 10 m.
Koľko kg farby potrebujeme na natretie stĺpa tvaru pravidelného trojbokého hranola s hranou podstavy dlhou 2,5 m a výškou na hranu podstavy 2 m, ak 1 kg farby vystačí na 25 m² náteru? Stĺp je vysoký 10 m. - Koeficient podobnosti
 Daný je trojuholník ABC so stranami a=12 cm b=9 cm c=7cm a trojuholník DEF so stranami d=8,4 cm, e=6,3 cm f=4,9 cm Zisti či sú trojuholníky ABC a DEF podobné ak áno koeficient podobnosti a napíš podľa ktorej vety sú podobné
Daný je trojuholník ABC so stranami a=12 cm b=9 cm c=7cm a trojuholník DEF so stranami d=8,4 cm, e=6,3 cm f=4,9 cm Zisti či sú trojuholníky ABC a DEF podobné ak áno koeficient podobnosti a napíš podľa ktorej vety sú podobné - Ženy vo firme
 V továrni pracuje 1467 žien. Ženy tvoria 46% všetkých zamestnancov továrne.Koľko zamestnancov pracuje v továrni?
V továrni pracuje 1467 žien. Ženy tvoria 46% všetkých zamestnancov továrne.Koľko zamestnancov pracuje v továrni? - Voda + teplota
 Voda o hmotnosti 5 kg a počiatočnej teplote 20°C sme dodali teplo 1365 kJ. Na akú teplotu sa ohriala?
Voda o hmotnosti 5 kg a počiatočnej teplote 20°C sme dodali teplo 1365 kJ. Na akú teplotu sa ohriala? - Natierači 5
 Šesť natieračov malo v plánovanej lehote natrieť 6000 m² plochy. Dvaja natierači ochoreli, takže každý zo štyroch, ktorí zostali, musí natrieť každý deň o 50 m² viac oproti plánovanému dennému výkonu. Vypočítajte, aký bol pôvodný plánovaný denný výkon jed
Šesť natieračov malo v plánovanej lehote natrieť 6000 m² plochy. Dvaja natierači ochoreli, takže každý zo štyroch, ktorí zostali, musí natrieť každý deň o 50 m² viac oproti plánovanému dennému výkonu. Vypočítajte, aký bol pôvodný plánovaný denný výkon jed - Jána a Tomáš
 Jana a Tomáš dostali dohromady od babičky 105 Kč. Jana dostala o tretinu viac ako Tomáš. O koľko Kč (korún) dostal Tomáš menej ako Jana?
Jana a Tomáš dostali dohromady od babičky 105 Kč. Jana dostala o tretinu viac ako Tomáš. O koľko Kč (korún) dostal Tomáš menej ako Jana? - Aký veľký 4
 Aký veľký uhol je keď jedna strana má 20m a druhá má 1,5m pri pravoúhlom trojuholníku?
Aký veľký uhol je keď jedna strana má 20m a druhá má 1,5m pri pravoúhlom trojuholníku? - V knižnici
 Máme 8 rôznych kníh v knižnici. Koľkými spôsobmi ich možno zoradiť? Koľko je možnosťou, ak majú byť 3 zväzky v určitom poradí? Koľko je možnosťou, ak majú byť tri zväzky za sebou nezávisle v poradí?
Máme 8 rôznych kníh v knižnici. Koľkými spôsobmi ich možno zoradiť? Koľko je možnosťou, ak majú byť 3 zväzky v určitom poradí? Koľko je možnosťou, ak majú byť tri zväzky za sebou nezávisle v poradí? - Trávova zmes
 Peter plánuje nakúpiť trávovu zmes zloženú zo semena lipnice a kostravy za 40 eur. 1 kg lipnice stojí 6 eur a 1 kg kostravy stojí 10 eur. Koľko ktorej zložky má kúpiť, ak výsledna zmes má mať hmotnosť 6kg?
Peter plánuje nakúpiť trávovu zmes zloženú zo semena lipnice a kostravy za 40 eur. 1 kg lipnice stojí 6 eur a 1 kg kostravy stojí 10 eur. Koľko ktorej zložky má kúpiť, ak výsledna zmes má mať hmotnosť 6kg? - Ľad + voda
 Obdlžnikove klzisko s rozmermi 60 m a 30 m malo vrstvu ľadu výšky 3 cm koľko litrov vody bolo na vytvorenie ľadu?
Obdlžnikove klzisko s rozmermi 60 m a 30 m malo vrstvu ľadu výšky 3 cm koľko litrov vody bolo na vytvorenie ľadu? - Zelenina - slizeň
 Súkromný pestovateľ zeleniny žne úrodu 12 hodín, jeho syn za 10 hodín. Ako dlho budú žať úrodu spoločne?
Súkromný pestovateľ zeleniny žne úrodu 12 hodín, jeho syn za 10 hodín. Ako dlho budú žať úrodu spoločne? - Malý úrok 3
 Tomáš mal na účte istú sumu peňazí, ktorá mu za rok priniesla úrok 64 € pri úrokovej miere 2% p. a. Aký by bol úrok z tej istej sumy, ak by ročná úroková miera bola 3,5 %?
Tomáš mal na účte istú sumu peňazí, ktorá mu za rok priniesla úrok 64 € pri úrokovej miere 2% p. a. Aký by bol úrok z tej istej sumy, ak by ročná úroková miera bola 3,5 %? - Rovnosť momentov
 Páka s hmotnosťou 3 kg a dĺžkou 2 m je zaťažená na konci závažiami s hmotnosťami 5 kg a 8 kg. Nájdite miesto, kde treba páku podoprieť, aby bola v rovnováhe.
Páka s hmotnosťou 3 kg a dĺžkou 2 m je zaťažená na konci závažiami s hmotnosťami 5 kg a 8 kg. Nájdite miesto, kde treba páku podoprieť, aby bola v rovnováhe. - 4B - zrezaný ihlan
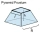 Vypočítajte objem pravidelného zrezaneho štvorbokého ihlana ak podstavné hrany sú 10cm a 4cm a výška bočnej steny je 5cm?
Vypočítajte objem pravidelného zrezaneho štvorbokého ihlana ak podstavné hrany sú 10cm a 4cm a výška bočnej steny je 5cm? - Robotník 8
 Robotník má pracovnú normu 15 výrobkov za 8 hodín, vyrobil ich za 6,5 hodiny. Na koľko % splnil plán?
Robotník má pracovnú normu 15 výrobkov za 8 hodín, vyrobil ich za 6,5 hodiny. Na koľko % splnil plán?
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
