Príklady na lichobežník - strana 4 z 15
Počet nájdených príkladov: 293
- Vypočítajte rovnoramenný
 Vypočítajte dĺžku ramien a obsah rovnoramenného lichobežníka, ak poznáte nasledujúce parametre: o = 20 cm a = 10 cm, c = 4 cm v = 2 cm
Vypočítajte dĺžku ramien a obsah rovnoramenného lichobežníka, ak poznáte nasledujúce parametre: o = 20 cm a = 10 cm, c = 4 cm v = 2 cm - Slnečnica
 Slnečnicové pole tvaru lichobežníka sa nachádza medzi dvoma rovnobežnými cestami, ktoré sú od seba vzdialené 230m. Dĺžky rovnobežných strán poľa sú 255m a 274m. Koľko ton slnečnice sa približne urodí na tomto poli, ak je hektárový výnos 2,25tony?
Slnečnicové pole tvaru lichobežníka sa nachádza medzi dvoma rovnobežnými cestami, ktoré sú od seba vzdialené 230m. Dĺžky rovnobežných strán poľa sú 255m a 274m. Koľko ton slnečnice sa približne urodí na tomto poli, ak je hektárový výnos 2,25tony? - Záhradka 7
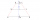 Záhradka tvaru lichobežníka má základne dĺžky 44 m a 16 m, ich vzdialenosť je 25 m. Koľko štvorcových metrov jej výmery zostane na výsadbu stromov, ak 1/5 celej plochy bude využitá na stavbu chaty, vybudovanie dvorčeka a cesty. Dá sa z daných údajov zisti
Záhradka tvaru lichobežníka má základne dĺžky 44 m a 16 m, ich vzdialenosť je 25 m. Koľko štvorcových metrov jej výmery zostane na výsadbu stromov, ak 1/5 celej plochy bude využitá na stavbu chaty, vybudovanie dvorčeka a cesty. Dá sa z daných údajov zisti - MO Z9–I–2 - 2017
 V lichobežníku VODY platí, že VO je dlhšou základňou, priesečník uhlopriečok K delí úsečku VD v pomere 3:2 a obsah trojuholníka KOV je rovný 13,5 cm². Určte obsah celého lichobežníka.
V lichobežníku VODY platí, že VO je dlhšou základňou, priesečník uhlopriečok K delí úsečku VD v pomere 3:2 a obsah trojuholníka KOV je rovný 13,5 cm². Určte obsah celého lichobežníka. - Vypočítajte 72
 Vypočítajte obsah lichobeznika so zakladňami a = 24cm, c =16 cm a uhlopriečkami u= 22 cm, v = 26 cm.
Vypočítajte obsah lichobeznika so zakladňami a = 24cm, c =16 cm a uhlopriečkami u= 22 cm, v = 26 cm. - Záhadný obsah
 Je daný lichobežník ABCD. Vypočítaj jeho obsah, ak plocha trojuholníka DBC je 27 cm².
Je daný lichobežník ABCD. Vypočítaj jeho obsah, ak plocha trojuholníka DBC je 27 cm². - Dokážte
 Lichobežník ABCD so základňami AB=a, CD=c má výšku v. Bod S je stred ramena BC. Dokážte že obsah trojuholníka ASD sa rovná polovici obsahu lichobežníka ABCD.
Lichobežník ABCD so základňami AB=a, CD=c má výšku v. Bod S je stred ramena BC. Dokážte že obsah trojuholníka ASD sa rovná polovici obsahu lichobežníka ABCD. - Vpísaná guľa
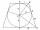 Do zrezaného komolého kužeľa s priemerom podstav D1=10 cm a D2=20 cm, je vpísaná guľa, ktorá sa dotýka oboch podstav i plášťa. Aký je jej priemer?
Do zrezaného komolého kužeľa s priemerom podstav D1=10 cm a D2=20 cm, je vpísaná guľa, ktorá sa dotýka oboch podstav i plášťa. Aký je jej priemer? - Pokrývanie strechy
 Strecha má tvar lichobežníka so základňami dĺžky 15m a 10m, výška strechy je 4m. Koľko škridlí budeme potrebovať, ak na 1m² treba 8 kúskov škridle?
Strecha má tvar lichobežníka so základňami dĺžky 15m a 10m, výška strechy je 4m. Koľko škridlí budeme potrebovať, ak na 1m² treba 8 kúskov škridle? - Jama
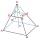 Jama v tvare zrezaného ihlana s obdlžnikovimi podstavami je hlboká 0,6 m. Dĺžka a šírka jamy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natretie 1 metra štvorcového jamy je treba 0,4 l zelenej farby. Koľko litrov farby sa na jej natretie použi
Jama v tvare zrezaného ihlana s obdlžnikovimi podstavami je hlboká 0,6 m. Dĺžka a šírka jamy je navrchu 3 × 1,5 m, dole 1 m × 0,5 m. Na natretie 1 metra štvorcového jamy je treba 0,4 l zelenej farby. Koľko litrov farby sa na jej natretie použi - Tehlový
 Tehlový pilier má tvar štvorbokého hranola s podstavou rovnoramenného lichobežníka so stranami a = 55 cm, c = 33 cm, rameno b = 33 cm, výška lichobežníka va = 32,1 cm. Pilier je vysoký 1,9 m. Koľko tehiel sa použilo na jeho stavbu, ak jedna tehla má objem
Tehlový pilier má tvar štvorbokého hranola s podstavou rovnoramenného lichobežníka so stranami a = 55 cm, c = 33 cm, rameno b = 33 cm, výška lichobežníka va = 32,1 cm. Pilier je vysoký 1,9 m. Koľko tehiel sa použilo na jeho stavbu, ak jedna tehla má objem - Urč obsah
 Urč obsah lichobežníka ABCD, v ktorom platí: AB= 6cm, Obsah trojuholníka ABC= 15 cm2, obsah trojuholníka BCD= 20 cm2, AB||CD.
Urč obsah lichobežníka ABCD, v ktorom platí: AB= 6cm, Obsah trojuholníka ABC= 15 cm2, obsah trojuholníka BCD= 20 cm2, AB||CD. - Lichobežník KLMN 2
 Lichobežník KLMN má základňu KL 40cm, MN 16cm. Na základni KL leží bod P. Úsečka NP rozdelí lichobežník na útvary o rovnakých obsahoch. Aká je vzdialenosť bodu P od bodu K?
Lichobežník KLMN má základňu KL 40cm, MN 16cm. Na základni KL leží bod P. Úsečka NP rozdelí lichobežník na útvary o rovnakých obsahoch. Aká je vzdialenosť bodu P od bodu K? - Archeológovia
 Archeológovia zistili, že vlajka bájneho matematického kráľovstva bola rozdelená na šesť políčok, tak ako na obrázku. V skutočnosti bola vlajka trojfarebná a každé políčko bolo vyfarbené jednou farbou. Vedci už vybádali, že na vlajke bola použitá červená,
Archeológovia zistili, že vlajka bájneho matematického kráľovstva bola rozdelená na šesť políčok, tak ako na obrázku. V skutočnosti bola vlajka trojfarebná a každé políčko bolo vyfarbené jednou farbou. Vedci už vybádali, že na vlajke bola použitá červená, - Lichobežník
 Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm² a obsah trojuholníka DKC je 10 cm². Vypočítajte obsah lichobežníka ABCD.
Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm² a obsah trojuholníka DKC je 10 cm². Vypočítajte obsah lichobežníka ABCD. - Výkop pre cestu
 Pri budovaní novej cesty bolo potrebné vyhĺbiť v teréne cestu dlhú 280m. Spodná šírka, kde vedie vozovka, bola 20m široká. Hore bol celý výkop široký 30m. Hĺbka výkopu je 6m. Koľko m³ zeminy bolo treba odstrániť?
Pri budovaní novej cesty bolo potrebné vyhĺbiť v teréne cestu dlhú 280m. Spodná šírka, kde vedie vozovka, bola 20m široká. Hore bol celý výkop široký 30m. Hĺbka výkopu je 6m. Koľko m³ zeminy bolo treba odstrániť? - Medzi
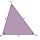 Medzi 3 stĺpiky je natiahnuté oceľové lanko. Výška prvého stĺpa je 4 m, výška druhého je 3,5m. Vzdialenosť prvých dvoch stĺpikov je 2,5m, vzdialenosť druhího a tretieho je 5m. Päty všetkých troch stĺpikov stojí v jednej priamke. Aká je výška tretieho stĺp
Medzi 3 stĺpiky je natiahnuté oceľové lanko. Výška prvého stĺpa je 4 m, výška druhého je 3,5m. Vzdialenosť prvých dvoch stĺpikov je 2,5m, vzdialenosť druhího a tretieho je 5m. Päty všetkých troch stĺpikov stojí v jednej priamke. Aká je výška tretieho stĺp - Podzemná
 Podzemná voda na zachytavanie dažďovej vody má tvar hranola s lichobežníkovými podstavami a=5 m, c=7 m vzdialenými od seba 4 metre. Hĺbka nádrže je 3 metre. Najviac koľko hektolitrov vody sa do nej zmestí, ak 8% jej objemu zaberá čerpadlo a potrubia?
Podzemná voda na zachytavanie dažďovej vody má tvar hranola s lichobežníkovými podstavami a=5 m, c=7 m vzdialenými od seba 4 metre. Hĺbka nádrže je 3 metre. Najviac koľko hektolitrov vody sa do nej zmestí, ak 8% jej objemu zaberá čerpadlo a potrubia? - Také tretinky
 Je daný lichobežníku ABCD s rovnobežnými stranami AB a CD pre bod E strany AB plati, že úsečka DE že delí lichobežník na dve časti s rovnakým obsahom. Spočítaj dĺžku úsečky AE.
Je daný lichobežníku ABCD s rovnobežnými stranami AB a CD pre bod E strany AB plati, že úsečka DE že delí lichobežník na dve časti s rovnakým obsahom. Spočítaj dĺžku úsečky AE. - Vypočítajte 21
 Vypočítajte koľko cukríkov sa zmestí do dózy tvaru 4-bokého hranola s podstavou lichobežníka s rozmermi základní 20 cm a 3,2 cm. Vzdialenosť základní je 50 mm. Dóza je vysoká 32 cm a 1 cukrík zaberie 2,5cm³ objemu.
Vypočítajte koľko cukríkov sa zmestí do dózy tvaru 4-bokého hranola s podstavou lichobežníka s rozmermi základní 20 cm a 3,2 cm. Vzdialenosť základní je 50 mm. Dóza je vysoká 32 cm a 1 cukrík zaberie 2,5cm³ objemu.
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
