Príklady na obvod kruhového oblúku - posledná strana
Počet nájdených príkladov: 34
- Uhol BSA
Je daná kružnica k (S; r) a bod A, ktorý leží na tejto kružnici. Na obvode leží aj bod B, pre ktorý platí, že je v jednom smere päťkrát ďalej od bodu A, než v opačnom smere (po obvode kružnice). Určte veľkosť konvexného uhla BSA. - Kružnicový oblúk 3
Dĺžka kružnicového oblúka prislúchajúceho uhlu s veľkosťou 120° je 8 cm. Aká je dĺžka celej kružnice? Aký je jej polomer? - Kruhový výsek a uhol
Aká je dĺžka oblúka kružnice s polomerom r=291 cm, ktorý prislúcha stredovému uhlu 135 °? Aký je obsah daného kruhového výseku? - Kruhový výsek
Kruhový výsek má obvod 186,05 mm a obsah 3814,07 mm2. Vypočítaj polomer príslušnej kružnice a veľkosť stredového uhla výseku. - Kruh - úsek
Rovnostrannému trojuholníku o strane 19 je vpísaná kruhový výsek, ktorého stred je v jednom z vrcholov trojuholníka a oblúk sa dotýka protiľahlej strany. Vypočítajte: a) dĺžku oblúka výseku b) pomer obvodu výseku ku obvodu trojuholníka - Železničný oblúk
Na turistickej mape s mierkou 1:50000 je úsek železničnej trate medzi Bobrovou Lhotou a Javořištěm nahradený oblúkom kružnice s polomerom 6 cm. Oblúk je 90°. Určite skutočnú dĺžku trate medzi oboma dedinami. - Oblúk - rozpon
Oblúk má polomer 3,3 m. Rozpon je 3,25 m a je 20 cm nad zemou. Aká dĺžka oblúka je potreba, aby oblúk dosiahol až na zem? - Odsek a oblúk
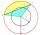Vypočítaj plochu S odseku a dľžku kružnicového oblúka l . Výška odseku je 2 cm a uhol α=60°. Pomôcka: S=1/2 r² . (β-sinβ) - Atletická trať - ovál
Dĺžka vnútorného okraja atletickej trate je 400 m. Rovné úseky meria 90 m. Vypočítaj rozmery ihriska - obdlžnika kam sa vojde tento ovál. - Minútová 4
Minútová ručička je dlhá 30 cm. Hodinová ručička je o polovicu kratšia ako minútová ručička. Akú veľkú dráhu opise jej koncovy bod za týždeň. - V 19.storočí
V 19-tom storočí bicykle nemali reťazový prevod a pedále boli spojené priamo s osou kolesa. To sa postupne zväčšovalo, až vznikli tzv. Vysoké bicykle (velocipédy) s priemerom predného kolesa až 1,5 metra, kým zadné malo iba 45 cm. V roku 1891 dosiahol Fre - Z8 – I – 3 MO 2018
Peter narysoval pravidelný šesťuholník, ktorého vrcholy ležali na kružnici dĺžky 16 cm. Potom pre každý vrchol tohto šesťuholníka narysoval kružnicu so stredom v tomto vrchole, ktorá prechádzala jeho dvoma susednými vrcholmi. Vznikol tak útvar ako na obrá - Stredovým 8010
Urči polomer podstavy kužeľa, ak sa jeho plášť rozvinie v kruhový výsek s polomerom „s"=10 a stredovým uhlom x=60°. r=?, o=? - Kužeľ a polkruh
Ak je plášť kužeľa polkruh, potom priemer podstavy kužeľa je rovnaký ako dĺžka jeho strany. Dokážte.
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
