Z8 – I – 3 MO 2018
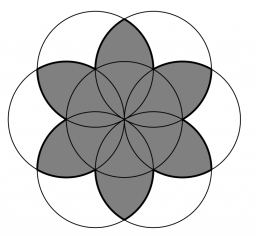
Peter narysoval pravidelný šesťuholník, ktorého vrcholy ležali na kružnici dĺžky 16 cm. Potom pre každý vrchol tohto šesťuholníka narysoval kružnicu so stredom v tomto vrchole, ktorá prechádzala jeho dvoma susednými vrcholmi.
Vznikol tak útvar ako na obrázku. Určte obvod vyznačeného kvietka
Vaša odpoveď:
Vznikol tak útvar ako na obrázku. Určte obvod vyznačeného kvietka
Vaša odpoveď:
Zobrazujem 6 komentárov:
Žiak
Dobrý deň. Ja som tento príklad pochopila tak, že kružnica má dľžku 16 cm. Potom by obvod kvetu bol 32 cm. Vy ste počítali tých 16 cm ako r - kružnice. Ako to vlastne je? Ďakujem za odpoveď.
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
planimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Štvorec a kružnica
Je daný štvorec a kružnica, ktorá prechádza dvoma susednými vrcholmi štvorca (krajnými bodmi strany a) a stredom protiľahlej strany (c). Ktorý z útvarov má väčší obvod? - Zostrojenie trojuholníka
Narysuj kružnicu k(S, r=3 cm). Zostroj trojuholník ABC tak, aby jeho vrcholy ležali na kružnici k a dĺžka strán bola (AB)=2,5 cm (AC)=4 cm - Pravidelný šesťuholník
Vypočítajte obvod pravidelného šesťuholníka s každou stranou 5 cm. - 6uholník - jednoduché
Obvod pravidelného šesťuholníka je 38. Určte polomer jeho opísanej kružnice. - Altánok
Vypočítaj v metroch štvorcových rozlohu altánku ktorého pôdorys má tvar pravidelného šestuholnika so stranou dĺžky 4,5 m. - Z7-1-6 MO 2018
Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj - Narysuj 4
Narýsuj úsečku KL=55 mm. Narýsuj kružnicu k so stredom K a polomerom 4 cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L.
