Z8 – I – 3 MO 2018
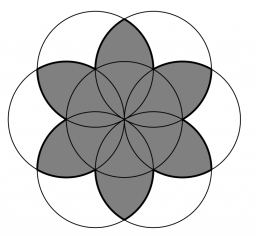
Petr narýsoval pravidelný šestiúhelník, jehož vrcholy ležely na kružnici délky 16 cm. Potom z každého vrcholu tohoto šestiúhelníku narýsoval kružnici, která procházela dvěma sousedními vrcholy. Vznikl tak útvar jako na následujícím obrázku.
Určete obvod vyznačeného kvítku.
Vaše odpověď:
Určete obvod vyznačeného kvítku.
Vaše odpověď:
Zobrazuji 5 komentářů:
Dava
Já jsem to napsal úplně jednoduše, prostě jsem si to kreslil. Na začátku jsem usekl kousek toho květu a pak jsem si určil jeho velikost
Snad vám to pomůže
Snad vám to pomůže
Žák
Kružnice délky 16 cm se skládá ze 6 oblouků stejné délky. Kvítek se skládá ze 12 týchž oblouků. Jeho obvod je tedy roven dvojnásobku obvodu kružnice.
5 let 1 Like
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- 6úhelník - jednoduché
Obvod pravidelného šestiúhelníku je 27. Určete poloměr jeho opsané kružnice. - Šestiúhelník ve kružnici
Vypočítejte poloměr kružnice, jejíž délka je o 10 cm větší než obvod pravidelného šestiúhelníku, který je vepsán do této kružnice. - Šestiúhelník - altánek
Vypočítej v metrech čtverečních rozlohu altánu jehož půdorys má tvar pravidelného šestiúhelníku se stranou délky 4,5 m. - Čtverec a kružnice
Je dán čtverec a kružnice, která prochází dvěma sousedními vrcholy čtverce (krajními body strany a) a středem protilehlé strany (c). Který z útvarů má větší obvod? - Trojúhelník konšt.
Narýsuj kružnici k(S, r=3 cm). Sestroj trojúhelník ABC tak , aby jeho vrcholy ležely na kružnici k a délka stran byla (AB)=2,5 cm (AC)=4 cm - Šestiúhelník
Je dán pravidelný šestiúhelník ABCDEF. Je-li obsah trojúhelníku ABC roven 16, pak obsah šestiúhelníku ABCDEF je roven? Nevím, jak na to jednoduše přijít.... - Šetiůhelník - hexagon
Vypočti obsah pravidelného šestiůhelníku o straně a=2 cm.
