Príklady na pravouhlý trojuholník - strana 21 z 86
Počet nájdených príkladov: 1702
- Patnactimetrový smrek
Patnactimetrovému smreku zlomila mohutná víchrica vršok tak, že zostal opierať o zem. Vzdialenosť tohto vŕšku od kmeňa bola 4,6 m dole. V akej výške bol kmeň smreku zlomený? - Narysuj 12
Narysuj rovnoramenný trojuholník ABC so základňou dlhou 7 cm a ramenami dlhými 5,5 cm. Zostroj všetky výšky, odmeraj ich a vypočítaj ich súčet - Ostrouhlý trojúholník
V ostrouhlom trojuholníku KLM je V priesečník jeho výšok a X je päta výšky na stranu KL. Os uhla XVL je rovnobežná so stranou LM a uhol MKL má veľkosť 70°. Akú veľkosť majú uhly KLM a KML? - V pravouhlom 8
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C poznáme dĺžku strany AB = 24 cm a uhol pri vrchole B = 71°. Vypočítajte dĺžku odvesien trojuholníka. - Adam oprel
Adam oprel rebrík o dom tak, že horný koniec dosahoval k oknu vo výške 3,6 m a dolný koniec stál na rovnej zemi a bol od steny odstavený o 1,5 m. Aká je dĺžka rebríka? - Peter a Pavol
Ako ďaleko od Petra stojí dvojmetrový Pavol? Peter sa na Pavla pozerá cez pravítko, ktoré drží v natiahnuté v ruke 60 cm od oka a na pravítku zmeral Pavlovu výšku na 15 mm. - Výška komína
Zo vzdialenosti 36 metrov od päty komína je vidieť jeho vrch pod uhlom 53 °. Vypočítaj výšku komína. Zaokrúhli na dm. - Stúpanie trate
Stúpanie trate je 9 promile, vzdialenosť kilometrovej (na sklone) [AC] = je 560 m. Urči uhol alfa a vzdialenosť [AB] = výšku medzi A a B. A / | B/_____________C - Tieň - rozhľadňa
Aká vysoká je rozhľadňa, ak vrhá tieň dlhý 9,6 m presne v rovnakom okamihu, keď polmetrová tyč vrhá tieň dlhý 30 cm. - Ťažnice zo súradníc
Je daný trojuholník ABC: A[-6,6; 1,2], B[3,4; -5,6], C [2,8;4,2]. Vypočítajte dĺžky jeho ťažníc - Pravouhlý
Pravouhlý trojuholník KLM s pravým uhlom pri vrchole L, uhľom beta pri vrchole K a uhľom alfa u vrchole M. Uhol pri vrchole M = 65°, strana l = 17,5 cm. Pomôcť Pytagorovy vety a goniometrických funkciu vypočítate dĺžky všetkých strán a uhol pri vrchole K. - Za bezvetria
Za úplného bezvetria vzlietol balón a ostal stáť presne nad miestom, z ktorého vzlietol. To je od nás vzdialené 250 metrov. Do akej výšky balón vyletel, keď ho vidíme pod výškovým uhlom 25°? - Pomer obsahov TRN ABC
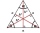V rovnostrannom trojuholníku ABC je bod T jeho ťažiskom, bod R je obrazom bodu T v osovej súmernosti, podľa priamky AB a bod N je obrazom bodu T v osovej súmernosti podľa priamky BC. Určte pomer obsahov trojuholníkov ABC a TRN. - Trojuholník KLM
Dané sú body K( -3; 2), L(-1; 4), M(3, -4). Zistite: a) či je trojuholník KLM pravouhlý b) vypočítajte dĺžku ťažnice na stranu k c) napíšte súradnice vektora LM d) napíšte smernicový tvar strany KM e) napíšte smernicový tvar osi strany KM - Telegrafný stĺp
Päty dvoch susedných telegrafných tyčí majú výškový rozdiel 10,5 m. Ako dlhé vodiče spájajú oba stĺpy, ak je sklon svahu 39° 30'? - Lietadlo 13
Lietadlo letiace práve nad miestom A vidieť z pozorovateľne B, vzdialenej od miesta A 2 400 metrov, vo výškovom uhle 52°30´. Ako vysoko letí lietadlo? - Hranica pozemku Pozemok má tvár pravouhlého trojuholníka s dĺžkou prepony 30 m. Obvod pozemku je 72 m. Akú dĺžku majú zostávajúce strany hranice pozemkov?
- Most
Z balónu, ktorý je 92 m nad mostom je vidieť jeden koniec mosta v hĺbkovom uhle 37° a druhý 30° 30'. Vypočítajte dĺžku mosta. - Rovnoramenný 22
Rovnoramenný trojuholník X'Y'Z' . Je podobný s trojuholníkom XYZ. Základňa trojuholníka XYZ má dĺžku |XY|=4 cm. Veľkosť uhla pri vrchole X je 45 stupňov. Narysuj trojuholník X'Y'Z', akého základňa má dĺžku 8 cm. - Pravouhlý trojuholník 8
Dĺžky strán dvoch trojuholníkov sme zoradili podľa veľkosti: 8 cm , 10 cm, 13 cm , 15 cm , 17 cm , 19 cm . Jeden z týchto dvoch trojuholníkov je pravouhlý. Vypočítajte obvod tohto pravouhlého trojuholníka v centimetroch
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
