Archeologové
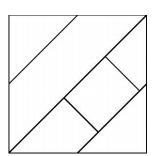
Archeologové zjistili, že vlajka bájného matematického království byla rozdělena na šest polí, tak jako na obrázku. Ve skutečnosti byla vlajka tříbarevná a každé pole bylo vybarveno jednou barvou. Vědci už vybádali, že na vlajce byla použita červená, bílá a modrá barva, že vnitřní obdélníkové pole bylo bílé a že spolu nesousedila dvě pole stejné barvy. Určete, kolik možností vzhledu vlajky musí archeologové v této fázi výzkumu zvažovat
Správná odpověď:
Zobrazuji 1 komentář:
Mo-radce
Nápověda. Začněte vybarvovat a zvažujte, kdy je následující postup jednoznačný a kdy existuje více možností.
Řešení. Trojúhelníkové pole sousedící s bílým obdélníkem může být buď červené, nebo modré:
Pokud by toto pole bylo červené, potom by pravoúhlé lichoběžníky musely být modré (sousedí s bílým obdélníkem a červeným trojúhelníkem) a poslední lichoběžníkové pole by muselo být červené (sousedí s bílým obdélníkem a modrými lichoběžníky). Zbylé trojúhelníkové pole by pak mohlo být buď bílé, nebo modré (sousedí s červeným lichoběžníkem).
Pokud by trojúhelníkové pole sousedící s bílým obdélníkem bylo modré, potom by příslušná diskuse byla velmi podobná předchozí, akorát by byly prohozeny barvy červená a modrá.
Celkem tedy dostáváme 2 + 2 = 4 možnosti, které musí archeologové zvažovat.
Řešení. Trojúhelníkové pole sousedící s bílým obdélníkem může být buď červené, nebo modré:
Pokud by toto pole bylo červené, potom by pravoúhlé lichoběžníky musely být modré (sousedí s bílým obdélníkem a červeným trojúhelníkem) a poslední lichoběžníkové pole by muselo být červené (sousedí s bílým obdélníkem a modrými lichoběžníky). Zbylé trojúhelníkové pole by pak mohlo být buď bílé, nebo modré (sousedí s červeným lichoběžníkem).
Pokud by trojúhelníkové pole sousedící s bílým obdélníkem bylo modré, potom by příslušná diskuse byla velmi podobná předchozí, akorát by byly prohozeny barvy červená a modrá.
Celkem tedy dostáváme 2 + 2 = 4 možnosti, které musí archeologové zvažovat.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Vlajka
Kolik procent zaujímá bílá barva na české vlajce? - Vlajka
Vlajka má být složena ze 3 různobarevných vodorovných pruhů. K dispozici jsou barvy: bílá, červená, modrá, zelená a žlutá. Určete: A) počet všech vlajek B) počet vlajek s modrým pruhem C) počet vlajek s modrým pruhem uprostřed D) počet vlajek, které nemaj - Vlajka
Děti si nechaly ušít klubovou vlajku. Červená barva pokryla z celkové plochy vlajky 2/20, modrá plocha pětinu, žlutá 19% z celkové plochy. Kolik % zaujímá zelená plocha? - Desetinných 48181
Anna používá 8,1 litru bílé a modré barvy k malování stěn své ložnice. 4/5 z tohoto množství je bílá barva a zbytek je modrá barva. Kolik půllitrů modré barvy použila na malování stěn ložnice? Vyjádřete svou odpověď ve tvaru zlomků a desetinných míst. Vyř
- CZ vlajka
Vypočítej obsahy barevných dílů na naší vlajce ve tvaru obdélníku o rozměrech 2m a 1m. Bílá a červená tvoří poloviny šířky, modrý trojúhelník je rovnoramenný a jeho vrchol je v polovině délky. - Kolik 17
Kolik procent česke vlajky tvoří modrá bílá a červená textílie? - Vlajky
Kolik různých vlajek lze vytvořit z látek barvy šedej, žltej, modrej, oranžovej, bielej, červenej, fialovej, zelenej tak aby každá vlajka se skládala ze tří různých barev?
