Z7–I–6, výstava koček
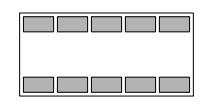
Na výstavě dlouhosrstých koček se sešlo celkem deset vystavujících. Vystavovalo se v obdélníkové místnosti, ve které byly dvě řady stolů jako na obrázku. Kočky byly označeny navzájem různými čísly v rozmezí 1 až 10 a na každém stole seděla jedna kočka. Určete, která kočka byla na výstavě hodnocena nejlépe, pokud víte, že:
a) součet čísel koček sedících naproti sobě byl vždy stejný,
b) součet čísel každých dvou koček sedících vedle sebe byl sudý,
c) součin čísel každých dvou koček sedících vedle sebe v dolní řadě je násobek čísla 8,
d) kočka číslo 1 není na kraji a je víc vpravo než kočka číslo 6,
e) vyhrála kočka sedící v pravém dolním rohu.
Vaše odpověď:
a) součet čísel koček sedících naproti sobě byl vždy stejný,
b) součet čísel každých dvou koček sedících vedle sebe byl sudý,
c) součin čísel každých dvou koček sedících vedle sebe v dolní řadě je násobek čísla 8,
d) kočka číslo 1 není na kraji a je víc vpravo než kočka číslo 6,
e) vyhrála kočka sedící v pravém dolním rohu.
Vaše odpověď:
Zobrazuji 1 komentář:
Mo-radca
Nápověda. Může proti sobě, příp. vedle sebe sedět kočka se sudým a kočka s lichým
číslem?
Možné řešení. Postupně rozebereme důsledky jednotlivých poznatků ze zadání:
a) Čísla koček sedících proti sobě tvoří 5 párů se stejným součtem. Součet čísel všech koček je 1 + 2 + . . . + 10 = 55, takže každý pár musí mít součet 55 : 5 = 11; jediné možnosti jsou 1 + 10, 2 + 9, 3 + 8, 4 + 7, 5 + 6.
b) Sudé číslo nelze získat součtem sudého a lichého čísla. V jedné řadě proto mohou sedět pouze kočky s lichými čísly, ve druhé pouze kočky se sudými čísly.
c) Násobek čísla 8 nelze získat součinem lichých čísel. Odtud a z předchozího důsledku plyne, že v dolní řadě seděly pouze kočky se sudými čísly, tj. 2, 4, 6, 8, 10. Součinem dvou takových čísel lze získat násobek 8, právě když jeden ze součinitelů je 4 nebo 8. Proto nemohou být kočky s čísly 4 a 8 na krajích, ani uprostřed.
d) Podle důsledku a) víme, že proti kočce s číslem 1 seděla kočka s číslem 10. Odtud plyne, že také kočka s číslem 10 nemůže být na kraji a je víc vpravo než kočka s číslem 6.
e) Z dosavadních informací víme, že v pravém dolním rohu seděla kočka se sudým číslem různým od 4, 8, 10 a 6.
Vyhrála tedy kočka s číslem 2.
Poznámka. Z uvedeného téměř umíme určit rozmístění všech koček v místnosti: pořadí koček ve spodní řadě mohlo být
buď 6, 4, 10, 8, 2, nebo 6, 8, 10, 4, 2, pořadí koček v horní řadě je pak jednoznačně určeno podle důsledku a).
číslem?
Možné řešení. Postupně rozebereme důsledky jednotlivých poznatků ze zadání:
a) Čísla koček sedících proti sobě tvoří 5 párů se stejným součtem. Součet čísel všech koček je 1 + 2 + . . . + 10 = 55, takže každý pár musí mít součet 55 : 5 = 11; jediné možnosti jsou 1 + 10, 2 + 9, 3 + 8, 4 + 7, 5 + 6.
b) Sudé číslo nelze získat součtem sudého a lichého čísla. V jedné řadě proto mohou sedět pouze kočky s lichými čísly, ve druhé pouze kočky se sudými čísly.
c) Násobek čísla 8 nelze získat součinem lichých čísel. Odtud a z předchozího důsledku plyne, že v dolní řadě seděly pouze kočky se sudými čísly, tj. 2, 4, 6, 8, 10. Součinem dvou takových čísel lze získat násobek 8, právě když jeden ze součinitelů je 4 nebo 8. Proto nemohou být kočky s čísly 4 a 8 na krajích, ani uprostřed.
d) Podle důsledku a) víme, že proti kočce s číslem 1 seděla kočka s číslem 10. Odtud plyne, že také kočka s číslem 10 nemůže být na kraji a je víc vpravo než kočka s číslem 6.
e) Z dosavadních informací víme, že v pravém dolním rohu seděla kočka se sudým číslem různým od 4, 8, 10 a 6.
Vyhrála tedy kočka s číslem 2.
Poznámka. Z uvedeného téměř umíme určit rozmístění všech koček v místnosti: pořadí koček ve spodní řadě mohlo být
buď 6, 4, 10, 8, 2, nebo 6, 8, 10, 4, 2, pořadí koček v horní řadě je pak jednoznačně určeno podle důsledku a).
10 let 3 Likes
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
témaÚroveň náročnosti úkolu
Související a podobné příklady:
- Stoly v salonku
U nezkrotného divočáka měli před bitvou třicet stolů označených přirozenými čísly 2 až 31. Právě dva stoly patřily do salonku. Aby personál při inventuře zjistil, které dva to jsou, používal trik. Na dveřích salonku byla tabulka s číslem, které nebylo děl - Největší číslo
Najděte největší číslo takové, že: 1.žádná číslice se v něm neopakuje, 2.součin každých dvou číslic je lichý, 3.součet všech číslic je sudý. - V řadě
V řadě čtyř čísel je rozdíl každých dvou sousedních čísel roven třem. Součet těchto čísel je 60. Určete tato čísla. - Danka a janka
Dvojčata Danka a Janka šli s kamarádkou Betkou do kina. V kině bylo volných už jen 6 sedadel ve druhé řadě. Kolik mají možností usazení, když dvojčata chtějí sedět vedle sebe, Danka vždy vpravo od Janky a Betka při jedné z nich? - Třída
Kolika různými způsoby mohou sedět vedle sebe 6 chlapců a 5 dívek, pokud chtějí dívky sedět na kraji? - Petra 3 MO 2022
Petra měla napsaná přirozená čísla od 1 do 9. Dvě z těchto čísel sečetla, smazala a výsledný součet napsala místo sčítanců. Měla tak napsáno osm čísel, která se jí podařilo rozdělit do dvou skupin se stejným součinem. Určete jaký největší mohl být tento s - Mirek a Zuzka
Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3. Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich m
