Z7–I–6, výstava mačiek
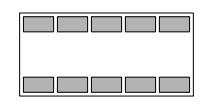
Na výstave dlhosrstých mačiek sa zišlo celkom desať vystavujúcich. Vystavovalo sa v obdĺžnikovej miestnosti, v ktorej boli dva rady stolov ako na obrázku. Mačky boli označené navzájom rôznymi číslami v rozmedzí 1 až 10 a na každom stole sedela jedna mačka. Určite, ktorá mačka bola na výstave hodnotená najlepšie, ak viete, že:
a) súčet čísel mačiek sediacich oproti sebe bol vždy rovnaký,
b) súčet čísel každých dvoch mačiek sediacich vedľa seba bol párny,
c) súčin čísel každých dvoch mačiek sediacich vedľa seba v dolnej rade je násobok čísla 8,
d) mačka číslo 1 nie je na kraji a je viac vpravo než mačka číslo 6,
e) vyhrala mačka sediaci v pravom dolnom rohu.
a) súčet čísel mačiek sediacich oproti sebe bol vždy rovnaký,
b) súčet čísel každých dvoch mačiek sediacich vedľa seba bol párny,
c) súčin čísel každých dvoch mačiek sediacich vedľa seba v dolnej rade je násobok čísla 8,
d) mačka číslo 1 nie je na kraji a je viac vpravo než mačka číslo 6,
e) vyhrala mačka sediaci v pravom dolnom rohu.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo-radca
Nápoveda. Môže proti sebe, príp. vedľa seba sedieť mačka s párnym a mačka s nepárnym číslom?
Možné riešenie. Postupne rozoberieme dôsledky jednotlivých poznatkov zo zadania:
a) Čísla mačiek sediacich proti sebe tvorí 5 párov s rovnakým súčtom. Súčet čísel všetkých mačiek je 1 + 2 +. . . + 10 = 55, takže každý pár musí mať súčet 55: 5 = 11; jediné možnosti sú 1 + 10, 2 + 9, 3 + 8, 4 + 7, 5 + 6.
b) Párne číslo nemožno získať súčtom párneho a nepárneho čísla. V jednom rade preto môžu sedieť len mačky s nepárnymi číslami, v druhej iba mačky s párnymi číslami.
c) Násobok čísla 8 nemožno získať súčinom nepárnych čísel. Odtiaľ a predchádzajúceho dôsledku vyplýva, že v dolnom rade sedeli iba mačky s párnymi číslami, tj. 2, 4, 6, 8, 10. Súčinom dvoch takých čísel možno získať násobok 8, práve keď jeden zo súčiniteľov je 4 alebo 8. Preto nemôžu byť mačky s číslami 4 a 8 na krajoch, ani uprostred.
d) Podľa dôsledku a) vieme, že proti mačke s číslom 1 sedela mačka s číslom 10. Odtiaľ vyplýva, že tiež mačka s číslom 10 nemôže byť na kraji a je viac vpravo než mačka s číslom 6.
e) Z doterajších informácií vieme, že v pravom dolnom rohu sedela mačka s párnym číslom rôznym od 4, 8, 10 a 6.
Vyhrala teda mačka s číslom 2.
Poznámka. Z uvedeného takmer vieme určiť rozmiestnenie všetkých mačiek v miestnosti: poradie mačiek v spodnej rade mohlo byť buď 6, 4, 10, 8, 2, alebo 6, 8, 10, 4, 2, poradie mačiek v hornom rade je potom jednoznačne určené podľa dôsledku a).
Možné riešenie. Postupne rozoberieme dôsledky jednotlivých poznatkov zo zadania:
a) Čísla mačiek sediacich proti sebe tvorí 5 párov s rovnakým súčtom. Súčet čísel všetkých mačiek je 1 + 2 +. . . + 10 = 55, takže každý pár musí mať súčet 55: 5 = 11; jediné možnosti sú 1 + 10, 2 + 9, 3 + 8, 4 + 7, 5 + 6.
b) Párne číslo nemožno získať súčtom párneho a nepárneho čísla. V jednom rade preto môžu sedieť len mačky s nepárnymi číslami, v druhej iba mačky s párnymi číslami.
c) Násobok čísla 8 nemožno získať súčinom nepárnych čísel. Odtiaľ a predchádzajúceho dôsledku vyplýva, že v dolnom rade sedeli iba mačky s párnymi číslami, tj. 2, 4, 6, 8, 10. Súčinom dvoch takých čísel možno získať násobok 8, práve keď jeden zo súčiniteľov je 4 alebo 8. Preto nemôžu byť mačky s číslami 4 a 8 na krajoch, ani uprostred.
d) Podľa dôsledku a) vieme, že proti mačke s číslom 1 sedela mačka s číslom 10. Odtiaľ vyplýva, že tiež mačka s číslom 10 nemôže byť na kraji a je viac vpravo než mačka s číslom 6.
e) Z doterajších informácií vieme, že v pravom dolnom rohu sedela mačka s párnym číslom rôznym od 4, 8, 10 a 6.
Vyhrala teda mačka s číslom 2.
Poznámka. Z uvedeného takmer vieme určiť rozmiestnenie všetkých mačiek v miestnosti: poradie mačiek v spodnej rade mohlo byť buď 6, 4, 10, 8, 2, alebo 6, 8, 10, 4, 2, poradie mačiek v hornom rade je potom jednoznačne určené podľa dôsledku a).
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Najväčšie číslo
Nájdite najväčšie číslo také, že: 1.Žiadne číslice sa v ňom neopakuje, 2.súčin každých dvoch číslic je nepárny, 3.súčet všetkých číslic je párny. - Obdĺžnik - kto má pravdu
Obdĺžnik je rozdelený na 7 políčok. Na každé políčko sa má napísať práve jedno z čísel 1, 2 a 3. Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto - MO Z6–I–3 2018
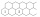Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude - Kino 10
Dvojičky Danka a Janka išli s kamarátkou Betkou do kina. V kine bolo voľných už len 6 sedadiel v druhom rade. Koľko majú možností usadenia, ak dvojičky chcú sedieť vedľa seba, Danka vždy vpravo od Janky a Betka pri jednej z nich?
- Richardove čísla Z8-I-2 2019
Richard sa pohrával s dvoma päťcifernými číslami. Každé pozostávalo z navzájom rôznych cifier, ktoré pri jednom boli všetky nepárne a pri druhom všetky párne. Po chvíli zistil, že súčet týchto dvoch čísel začína dvojčíslím 11 a končí číslom 1 a že ich roz - Štyrikrát 3453
Súčin dvoch čísel sa rovná ich súčtu. Jedno z čísel je štyrikrát väčšie ako druhé číslo. Určite tieto čísla, ak viete že žiadne z nich sa nerovná nule. - Ľaváčka
Eva, Lucia, Barbora, Ivana a Slávka sú dobré kamarátky, preto na hodine biológie chcú vždy sedieť pri jednom dlhom stole vedľa seba. Koľkými spôsobmi sa môžu posadiť, ak Slávka je ľaváčka, a preto chce vždy sedieť na ľavom kraji stola?
