Mirek a Zuzka
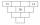
Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3.
Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich má pravdu.
Výsledek
Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich má pravdu.
Výsledek
Zobrazuji 1 komentář:
Mo-radca
Nápověda. Zjistěte, které různé součty lze získat.
Možné řešení. Všechny možné dvojice, které lze z daných čísel složit, jsou (1,1); (1,2),(2,1); (1,3),(2,2),(3,1); (2,3),(3,2); (3,3).
Tyto možnosti dávají 5 různých součtů, a to 2, 3, 4, 5, 6 (dvojice s různými součty jsou odděleny středníky). Na uvedeném obrázku však potřebujeme 6 dvojic s různými součty, pravdu má tedy Zuzka.
Poznámky.
a) K určení možných součtů není třeba vypisovat všechny přípustné dvojice:
nejmenší součet odpovídá 1 + 1 = 2, největší je 3 + 3 = 6. Odtud plyne, že možných součtů není víc než 5, což je méně než požadovaných 6.
b) Řešení úlohy pomocí všech možných vyplnění tabulky a kontrolou takto získaných součtů je extrémně pracné. Pokud by však takové řešení bylo úplné, nechť je považováno za správne.
Možné řešení. Všechny možné dvojice, které lze z daných čísel složit, jsou (1,1); (1,2),(2,1); (1,3),(2,2),(3,1); (2,3),(3,2); (3,3).
Tyto možnosti dávají 5 různých součtů, a to 2, 3, 4, 5, 6 (dvojice s různými součty jsou odděleny středníky). Na uvedeném obrázku však potřebujeme 6 dvojic s různými součty, pravdu má tedy Zuzka.
Poznámky.
a) K určení možných součtů není třeba vypisovat všechny přípustné dvojice:
nejmenší součet odpovídá 1 + 1 = 2, největší je 3 + 3 = 6. Odtud plyne, že možných součtů není víc než 5, což je méně než požadovaných 6.
b) Řešení úlohy pomocí všech možných vyplnění tabulky a kontrolou takto získaných součtů je extrémně pracné. Pokud by však takové řešení bylo úplné, nechť je považováno za správne.
7 let 2 Likes
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Z9–I–4 MO 2017
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p - Vláček
Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakem. Vlak měl tři vagony a v každém se vezla právě tři čísla. Číslo 1 se vezlo v prvním vagonu a v posledním vagonu byla všechna čísla lichá. Průvodčí cestou spočítal součet čísel v prvním, druhém i posledním vagonu - C–I–4 MO 2017
Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla. - Na papíře
Na papíře bylo napsáno několik kladných celých čísel. Miška si pamatovala pouze to, že každé číslo bylo polovinou součtu všech ostatních čísel. Kolik čísel mohlo být napsaných na papíře? - Pyramida Z8–I–6
Každá cihlička následující pyramidy obsahuje jedno číslo. Kdykoli to je možné, je číslo v každé cihličce nejmenším společným násobkem čísel ze dvou cihliček ležících přímo na ní. Které číslo může být v nejspodnější cihličce? Určete všechny možnosti. - Fourland 3542
V zemi Fourland mají pouze čtyři písmena F, O, U, R a každé slovo má právě čtyři písmena. V žádném slově se nesmí opakovat ani jedno písmeno. Napiš všechna slova, která se dají u nich napsat. - Vnučka
V roce 2014 byl součet věku Mecháčovy tety, její dcery a její vnučky roven 100 let. V kterém roce se narodila vnučka, pokud víme, že věk každé z nich lze vyjádřit jako mocnina dvou? - Z7–I–6, výstava koček
Na výstavě dlouhosrstých koček se sešlo celkem deset vystavujících. Vystavovalo se v obdélníkové místnosti, ve které byly dvě řady stolů jako na obrázku. Kočky byly označeny navzájem různými čísly v rozmezí 1 až 10 a na každém stole seděla jedna kočka. Ur - Skupina
Skupina 10 děvčat se má rozdělit na dvě skupiny tak, aby v každé byli nejméně 4 děvčata. Kolika způsoby to lze provést? - MO Z6–I–3 2018
Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políč - Z7–I–1 MO 2018
Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné číslo poskládané z těchto kartiček je dělitelné šesti. Navíc lze z těchto kartiček poskládat trojmístné číslo - Pozemek 10
Pozemek pana Častky má rozměry 252 dm a 28 m. Jak nejdále od sebe musí rozmístit kůly na plot, aby byly po obou stranách stejně daleko? Kolik jich bude potřebovat na oplocení celého pozemku? - MO Z6-6-1
Do prázdných polí v následujícím obrázku doplňte celá čísla větší než 1 tak, aby v každém tmavším políčku byl součin čísel ze sousedních světlejších políček: Jaké je číslo je středu? - Číselna osa
V kocourkovské škole používají zvláštní číselnou osu. Vzdálenost mezi čísly 1 a 2 je 1 cm, vzdálenost mezi čísly 2 a 3 je 3 cm, mezi čísly 3 a 4 je 5 cm, a tak dále, vzdálenost mezi následující dvojicí přirozenými čísly se vždy zvètší o 2 cm. Mezi kterými - Kupky
Anička má celkem 702 Kč. Peníze musí rozdělit na různý počet kupek tak, aby na každé kupce byl stejný počet Kč. Kolik má možností? - MO Z6-1-3 2017 šachovnica
Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H - Pan Cuketa
Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja
