Příklady pro středoškoláky - strana 176 z 225
Počet nalezených příkladů: 4490
- Roční příjmy
 Roční příjmy (v tisících eur) patnácti rodin jsou: 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200 Vypočítejte harmonický a geometrický průměr těchto příjmů rodin.
Roční příjmy (v tisících eur) patnácti rodin jsou: 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200 Vypočítejte harmonický a geometrický průměr těchto příjmů rodin. - Vnuk s dědou
 Vnuk s dědou si počítali kolik mají spolu let. Součin jejich let je 365. Kolik je součet jejich let?
Vnuk s dědou si počítali kolik mají spolu let. Součin jejich let je 365. Kolik je součet jejich let? - Kostky - objemy
 Hrana druhé kostky je o 2 cm větší, než hrana první kostky. Rozdíl objemů kostek je 728 cm³. Vypočítejte velikosti hran obou kostek.
Hrana druhé kostky je o 2 cm větší, než hrana první kostky. Rozdíl objemů kostek je 728 cm³. Vypočítejte velikosti hran obou kostek. - Dvě krabice
 Dvě krabice tvaru krychle s hranami a=57 cm, b=65 cm je třeba nahradit jednou krabicí tvaru kostky (stejného souhrnného objemu). Jaká bude její hrana?
Dvě krabice tvaru krychle s hranami a=57 cm, b=65 cm je třeba nahradit jednou krabicí tvaru kostky (stejného souhrnného objemu). Jaká bude její hrana? - Mosazná trubka
 Vnější obvod mosazné trubky (ρ = 8,5 g/cm³) je 38 cm. Její hmotnost je 6 kg a délka je 57 cm. Jaká je tloušťka stěny trubky?
Vnější obvod mosazné trubky (ρ = 8,5 g/cm³) je 38 cm. Její hmotnost je 6 kg a délka je 57 cm. Jaká je tloušťka stěny trubky? - Rovnostranný válec
 Rovnostranný válec (v = 2r) má objem V = 230 cm³. Vypočítejte povrch tohto valce.
Rovnostranný válec (v = 2r) má objem V = 230 cm³. Vypočítejte povrch tohto valce. - Tětiva AB
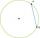 Jakou délku má tětiva AB, jejíž vzdálenost od středu S kružnice k (S, 20 cm) se rovná 10 cm?
Jakou délku má tětiva AB, jejíž vzdálenost od středu S kružnice k (S, 20 cm) se rovná 10 cm? - Léta
 Jirčinu bratrovi Mirkovi je 42 let. A je třikrát tak starý jako byla Jarka, když bylo Mirkovi tolik let kolik je Jarce nyní. Kolik je tedy Jarce.
Jirčinu bratrovi Mirkovi je 42 let. A je třikrát tak starý jako byla Jarka, když bylo Mirkovi tolik let kolik je Jarce nyní. Kolik je tedy Jarce. - Kruhová výseč
 Kruhová výseč se středovým úhlem 140° má obsah 50 cm². Určete její poloměr r.
Kruhová výseč se středovým úhlem 140° má obsah 50 cm². Určete její poloměr r. - Euklid 5
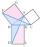 Vypočítejte strany pravoúhlého trojúhelníku ABC pokud: a = 7 cm, vc = 5 cm.
Vypočítejte strany pravoúhlého trojúhelníku ABC pokud: a = 7 cm, vc = 5 cm. - Konstrukce histogramu a svíčkového grafu
 Sestrojte histogramový a svíčkový graf pro dané údaje. 56, 32, 54, 32, 23, 67, 23, 45, 12, 32, 34, 24, 36, 47, 19, 43
Sestrojte histogramový a svíčkový graf pro dané údaje. 56, 32, 54, 32, 23, 67, 23, 45, 12, 32, 34, 24, 36, 47, 19, 43 - Čajová směs
 Čajové směsi jsou namíchány ze 2druhů čaje. Ve standartní čajové směsi jsou hmotnosti obou druhů čaje v poměru 1:3 a 40g balení stojí 42,-Kč. Ve výběrové čajové směsi jsou hmotnosti obou druhů čaje v poměru 1:1 a 50g balení stojí 60,-Kč. Kolik stojí 10g d
Čajové směsi jsou namíchány ze 2druhů čaje. Ve standartní čajové směsi jsou hmotnosti obou druhů čaje v poměru 1:3 a 40g balení stojí 42,-Kč. Ve výběrové čajové směsi jsou hmotnosti obou druhů čaje v poměru 1:1 a 50g balení stojí 60,-Kč. Kolik stojí 10g d - 3-průměr
 V případě, že průměr (aritmetický průměr) ze tří čísel x, y, z je 50. Jaký je průměr čísel (3x +10), (3y +10), (3z + 10)?
V případě, že průměr (aritmetický průměr) ze tří čísel x, y, z je 50. Jaký je průměr čísel (3x +10), (3y +10), (3z + 10)? - Krychle
 Krychli o hraně 1 m je opsána koule (vrcholy krychle leží na povrchu koule). Určete velikost povrchu teto koule.
Krychli o hraně 1 m je opsána koule (vrcholy krychle leží na povrchu koule). Určete velikost povrchu teto koule. - Dvojice
 Ve třídě je 34 žáků, z toho 14 chlapců a 20 dívek. Kolik dvojic (heterosexuálních, tedy kluk-dívka) můžeme vytvořit? Podle jakého vzorce?
Ve třídě je 34 žáků, z toho 14 chlapců a 20 dívek. Kolik dvojic (heterosexuálních, tedy kluk-dívka) můžeme vytvořit? Podle jakého vzorce? - Cifry A,B,C
 Pro různé cifry A,B,C platí: druhá odmocnina ze BC se rovná A a součet B+C se rovná A. Urči A+2B+3C. BC uvažujte ako dvojciferné číslo, nie jako súčin.
Pro různé cifry A,B,C platí: druhá odmocnina ze BC se rovná A a součet B+C se rovná A. Urči A+2B+3C. BC uvažujte ako dvojciferné číslo, nie jako súčin. - Zázračný strom
 Zázračný strom roste tak rychle, že se první den zvětší jeho výška o polovinu celkové výšky, druhý den o třetinu, třetí den o čtvrtinu, atd. Kolikrát se zvětší jeho výška za 6 dní?
Zázračný strom roste tak rychle, že se první den zvětší jeho výška o polovinu celkové výšky, druhý den o třetinu, třetí den o čtvrtinu, atd. Kolikrát se zvětší jeho výška za 6 dní? - Bonboniéra
 V bonboniéře je 12 bonbónů, které vypadají stejně. Tři z nich jsou plněné nugátem, čtyři oříškem a pět krémem. Nejméně kolik bonbónů musí Ivan vybrat, aby měl jistotu, že vybere dva se stejnou nádivkou?
V bonboniéře je 12 bonbónů, které vypadají stejně. Tři z nich jsou plněné nugátem, čtyři oříškem a pět krémem. Nejméně kolik bonbónů musí Ivan vybrat, aby měl jistotu, že vybere dva se stejnou nádivkou? - Hod kostkami
 Když házíš deseti kostkami najednou, tak v průměru hodíš 35. Kolik průměrně hodíš, pokud vždy když padne šestka házíš tou kostkou znovu?
Když házíš deseti kostkami najednou, tak v průměru hodíš 35. Kolik průměrně hodíš, pokud vždy když padne šestka házíš tou kostkou znovu? - Lineárni rovnica se zlomkama
 Řešte v R následující lineární rovnici: 4/10X+2/10X+1/6X+1/10X+400=X
Řešte v R následující lineární rovnici: 4/10X+2/10X+1/6X+1/10X+400=X
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
