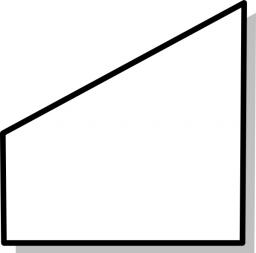
Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Trapezoidal prism
 Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Rectangular trapezoid
 The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Quadrilateral 80729
 Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD.
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Circumference 7052
 The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem
- Calculate square 2556
 Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square.
Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square. - Trapezoid 4908
 Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid.
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - Trapezium diagonals
 It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - IS trapezoid
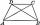 Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
- Trapezoid: 18703
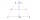 In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle.
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Perpendicular 32371
 Calculate the area of a rectangular trapezoid whose perpendicular arm is 27 mm long and the bases are 33 mm and 19 mm long.
Calculate the area of a rectangular trapezoid whose perpendicular arm is 27 mm long and the bases are 33 mm and 19 mm long. - Calculate 70814
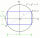 The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle. - Trapezoid IV
 In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD?
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD? - Calculate 2416
 In the rectangle ABCD we know the side length AB = 16 cm and the diagonal AC = 20 cm. Calculate its perimeter and area.
In the rectangle ABCD we know the side length AB = 16 cm and the diagonal AC = 20 cm. Calculate its perimeter and area.
- Rectangular trapezoid
 The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid. - Isosceles 37621
 In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - trapezium 3428
 Given is a trapezoid ABCD with bases AB, CD. Let K be side AB's midpoint, and point L be side CD's midpoint. The area of triangle ALB is 15 cm2, and the area of triangle DKC is 10 cm². Calculate the area of trapezium ABCD.
Given is a trapezoid ABCD with bases AB, CD. Let K be side AB's midpoint, and point L be side CD's midpoint. The area of triangle ALB is 15 cm2, and the area of triangle DKC is 10 cm². Calculate the area of trapezium ABCD.
