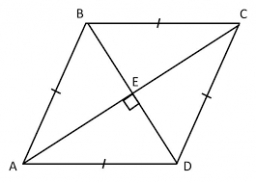
Diagonals of a rhombus 2
One diagonal of a rhombus is greater than the other by 4 cm. If the area of the rhombus is 96 cm2, find the side of the rhombus.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
- rhombus
- diagonal
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- PC and laptop
 A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at a 20% profit and the laptop at a 10% loss. If, overall, he made a 2% profit, then find the purchase price, in rupees, for the desktop.
A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at a 20% profit and the laptop at a 10% loss. If, overall, he made a 2% profit, then find the purchase price, in rupees, for the desktop. - 20 men
 20 men are supposed to complete a work in 10 days. After working for 5 days, they realize that only one-fourth of the work is done. How many more men they need to employ to complete the work on time?
20 men are supposed to complete a work in 10 days. After working for 5 days, they realize that only one-fourth of the work is done. How many more men they need to employ to complete the work on time? - The angles 5
 The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles.
The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles. - Bad weather
 An aircraft was slowed down during a 600 km flight due to bad weather. Its average speed was reduced by 200 km/hr from its usual speed, and the flight time increased by 30 minutes. Find the scheduled duration of the flight.
An aircraft was slowed down during a 600 km flight due to bad weather. Its average speed was reduced by 200 km/hr from its usual speed, and the flight time increased by 30 minutes. Find the scheduled duration of the flight.
- The enrolment 2
 The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment? - Violin and dance lesson
 Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of
Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of - EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
- The tangent of the hyperbola
 Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4].
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - Quadratic equation - Viets
 In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas.
In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas. - Two containers 2
 Two containers, one large and one small, contain a total of 4 kilograms of bath salts. One-quarter of the bath salts from the large container are transferred to the small container, so the ratio of bath salts in the large container to that in the small on
Two containers, one large and one small, contain a total of 4 kilograms of bath salts. One-quarter of the bath salts from the large container are transferred to the small container, so the ratio of bath salts in the large container to that in the small on - The sum 41
 The sum of 640.00 was deposited in the first bank for five years, and the interest given was 160.00. Find the rate.
The sum of 640.00 was deposited in the first bank for five years, and the interest given was 160.00. Find the rate. - Properties of eq2 roots
 If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
- Fredrik
 Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b.
Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b. - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle? - Flower shop
 In a flower shop, a bunch containing 3 tulips, 2 roses, and 1 daffodil cost $10.79. A different bunch containing 1 tulip, 2 roses, and 3 daffodils costs $10.13. A tulip costs 35 cents more than a rose. How much does 1 tulip and 1 rose, and 1 daffodil cost
In a flower shop, a bunch containing 3 tulips, 2 roses, and 1 daffodil cost $10.79. A different bunch containing 1 tulip, 2 roses, and 3 daffodils costs $10.13. A tulip costs 35 cents more than a rose. How much does 1 tulip and 1 rose, and 1 daffodil cost
