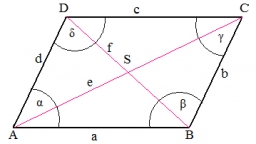
Diamond diagonals
Find the diamond diagonal's lengths if the area is 156 cm2 and the side is 13 cm long.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Diamond diagonals
 Calculate the diamond's diagonal lengths if its area is 156 cm² and the side length is 13 cm.
Calculate the diamond's diagonal lengths if its area is 156 cm² and the side length is 13 cm. - Diamond diagonals
 Calculate the diamonds' diagonal lengths if the diamond area is 156 cm square and the side length is 13 cm.
Calculate the diamonds' diagonal lengths if the diamond area is 156 cm square and the side length is 13 cm. - The diamond
 The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond.
The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond. - Two diagonals
 The diagonals of the diamond EFGH have lengths in the ratio of 1:2. What is the circumference of a rhombus if the longer diagonal is 8 cm long?
The diagonals of the diamond EFGH have lengths in the ratio of 1:2. What is the circumference of a rhombus if the longer diagonal is 8 cm long?
- Diamond side
 The diagonals of the diamond are 18 cm and 14 cm long. Calculate the length of the diamond side.
The diagonals of the diamond are 18 cm and 14 cm long. Calculate the length of the diamond side. - Diagonals of the rhombus
 How long are the diagonals e, and f in the diamond if its side is 5 cm long and its area is 20 cm²?
How long are the diagonals e, and f in the diamond if its side is 5 cm long and its area is 20 cm²? - Diagonals 5113
 In the diamond KLMN, the lengths of the diagonals are 10 cm and 6 cm. Determine the angle size that the longer diagonal makes with the side of the diamond.
In the diamond KLMN, the lengths of the diagonals are 10 cm and 6 cm. Determine the angle size that the longer diagonal makes with the side of the diamond. - The diamond
 The diamond has 35 cm-wide sides, and the diagonals are in a ratio of 1:2. Calculate the diagonal lengths.
The diamond has 35 cm-wide sides, and the diagonals are in a ratio of 1:2. Calculate the diagonal lengths. - Diamond
 Find the side of the diamond if its area is S = 490 cm² and one diagonal u2 = 39 cm.
Find the side of the diamond if its area is S = 490 cm² and one diagonal u2 = 39 cm.
- Kite
 John a kite, which is diamond-shaped. Its diagonals are 60 cm long and 90 cm long. Calculate: a) the diamond side b) how much paper John needs to make a kite if he needs a paper on both sides and needs 5% of the paper for bending?
John a kite, which is diamond-shaped. Its diagonals are 60 cm long and 90 cm long. Calculate: a) the diamond side b) how much paper John needs to make a kite if he needs a paper on both sides and needs 5% of the paper for bending? - Calculate: 16973
 The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend.
The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend. - Diagonals of a rhombus
 One of the diagonals of a rhombus is twice the other. If the sum of the lengths of the diagonals is 24, find the area of the rhombus.
One of the diagonals of a rhombus is twice the other. If the sum of the lengths of the diagonals is 24, find the area of the rhombus. - Rhombus and diagonals
 The lengths of the diamond diagonals are e = 48cm f = 20cm. Calculate the length of its sides.
The lengths of the diamond diagonals are e = 48cm f = 20cm. Calculate the length of its sides. - Diagonals
 A diagonal of a rhombus is 20 cm long. If its side is 26 cm, find the length of the other diagonal.
A diagonal of a rhombus is 20 cm long. If its side is 26 cm, find the length of the other diagonal.
- Rhombus diagonals
 In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, and calculate the area of the diamond.
In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, and calculate the area of the diamond. - Diagonals of a rhombus 2
 One diagonal of a rhombus is greater than the other by 4 cm. If the area of the rhombus is 96 cm2, find the side of the rhombus.
One diagonal of a rhombus is greater than the other by 4 cm. If the area of the rhombus is 96 cm2, find the side of the rhombus. - The diagonals
 The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond?
The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond?
