Circle + sphere - practice problems
Number of problems found: 28
- Float boya
 A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³.
A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³. - What is bigger?
 Which ball has a larger volume: a football with a circumference of 66 cm or a volleyball with a diameter of 20 cm?
Which ball has a larger volume: a football with a circumference of 66 cm or a volleyball with a diameter of 20 cm? - Average speed
 What is the average speed you have to move around the world in 80 days? (Path along the equator, round to km/h).
What is the average speed you have to move around the world in 80 days? (Path along the equator, round to km/h). - Determine 10561
 The hollow nickel ball has an outer diameter of 0.4 meters and an inner diameter of 0.3 meters. Determine its weight if the nickel density is 9000 kg/m³.
The hollow nickel ball has an outer diameter of 0.4 meters and an inner diameter of 0.3 meters. Determine its weight if the nickel density is 9000 kg/m³.
- Sphere
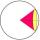 Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere. - Calculate 64734
 We cut a sphere with a diameter of 10 dm into two equal parts. Calculate the area of the cut.
We cut a sphere with a diameter of 10 dm into two equal parts. Calculate the area of the cut. - Circumference 61944
 Calculate the volume and surface of the planet Venus if its circumference is 12,000 km.
Calculate the volume and surface of the planet Venus if its circumference is 12,000 km. - Surface and volume
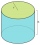 Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm.
Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm. - Metal balls
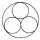 Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level?
Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level?
- Elevation
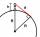 What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km. - The Earth
 The Earth's surface is 510,000,000 km². Calculates the radius, equator length, and volume of the Earth, assuming the Earth has the shape of a sphere.
The Earth's surface is 510,000,000 km². Calculates the radius, equator length, and volume of the Earth, assuming the Earth has the shape of a sphere. - One-quarter 46001
 Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm.
Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm. - Inscribed circle
 A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base? - Sphere cuts
 At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6?
At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6?
- Surveyors
 Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other?
Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other? - Earth's circumference
 Calculate the Earth's circumference of the parallel 48 degrees and 10 minutes.
Calculate the Earth's circumference of the parallel 48 degrees and 10 minutes. - Shortest 81627
 What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole?
What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole? - Intersection 40981
 The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere. - The volleyball ball
 The volleyball ball can have a circumference of at least 650 max 750 mm after inflation. What air volume can this ball hold if its circumference is the average of the minimum and maximum inflation of the ball?
The volleyball ball can have a circumference of at least 650 max 750 mm after inflation. What air volume can this ball hold if its circumference is the average of the minimum and maximum inflation of the ball?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
