Geometry - math word problems - page 153 of 162
Number of problems found: 3238
- Octagonal pyramid
 Draw an octagonal pyramid in free parallel projection if the length of the edge a = 3 cm and the height of the pyramid v = 6 cm.
Draw an octagonal pyramid in free parallel projection if the length of the edge a = 3 cm and the height of the pyramid v = 6 cm. - Eiffel Tower
 The Eiffel Tower in Paris is 300 meters high and made of steel. It weighs 8,000 tons. If the tower model made of the same material weighs 2.8 kg, how tall is it?
The Eiffel Tower in Paris is 300 meters high and made of steel. It weighs 8,000 tons. If the tower model made of the same material weighs 2.8 kg, how tall is it? - Extreme 5456
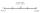 Draw line AB if you know one of its extreme points and the center of line S.
Draw line AB if you know one of its extreme points and the center of line S. - Perimeter - triangle
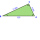 Construct triangle ABC when we know a + b + c (perimeter), height to side c, and angle gamma.
Construct triangle ABC when we know a + b + c (perimeter), height to side c, and angle gamma. - Circles
 How many different circles are determined by 14 points at the plane if 3 of them lie in a straight line?
How many different circles are determined by 14 points at the plane if 3 of them lie in a straight line? - Meneal's 26771
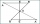 Show (using Meneal's theorem) that the center of gravity divides the line in a 1:2 ratio.
Show (using Meneal's theorem) that the center of gravity divides the line in a 1:2 ratio. - Ice + water
 A rectangular ice rink measuring 60 m by 30 m had a layer of ice 3 cm high. How many liters of water were used to create the ice?
A rectangular ice rink measuring 60 m by 30 m had a layer of ice 3 cm high. How many liters of water were used to create the ice? - In plane 2
 A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - Coefficient 81704
 In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4.
In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4. - Determine 8133
 Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh
Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh - Dice - 5 times
 We roll the dice five times. Make sentences: a) 3 events that definitely cannot happen. Write a reason for each. b) 3 events that will definitely occur; write a reason for each. Another problem: 3 events that may or may not occur for each. Write a reason.
We roll the dice five times. Make sentences: a) 3 events that definitely cannot happen. Write a reason for each. b) 3 events that will definitely occur; write a reason for each. Another problem: 3 events that may or may not occur for each. Write a reason. - Pipes
 The water pipe has a cross-section 1903 cm². An hour has passed 859 m³ of water. How much water flows through the pipe with cross-section 300 cm² per 11 hours if water flows at the same speed?
The water pipe has a cross-section 1903 cm². An hour has passed 859 m³ of water. How much water flows through the pipe with cross-section 300 cm² per 11 hours if water flows at the same speed? - Two forces
 The two forces, F1 = 580N and F2 = 630N, have an angle of 59 degrees. Calculate their resultant force, F.
The two forces, F1 = 580N and F2 = 630N, have an angle of 59 degrees. Calculate their resultant force, F. - Seawater
 Seawater density is 1025 kg/m³, and ice is 920 kg/m³. Eight liters of seawater froze and created a cube. Calculate the size of the cube edge.
Seawater density is 1025 kg/m³, and ice is 920 kg/m³. Eight liters of seawater froze and created a cube. Calculate the size of the cube edge. - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - View angle
 At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the river
At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the river - A man 7
 A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles toward N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.)
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles toward N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - Soap bubble
 A conductive soap bubble with a radius of r=2 cm and charged to a potential of φ= 10000 V will burst into a drop of water with a radius of r1= 0.05 cm. What is the potential φ1 of the drop?
A conductive soap bubble with a radius of r=2 cm and charged to a potential of φ= 10000 V will burst into a drop of water with a radius of r1= 0.05 cm. What is the potential φ1 of the drop? - Tower's view
 From the church tower's view at 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the house's height and its distance from the church.
From the church tower's view at 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the house's height and its distance from the church. - Shortest walk
 An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point
An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
