Geometry - math word problems - page 154 of 162
Number of problems found: 3238
- Forces
 Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant?
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant? - ABCDEFGHIJKL 8426
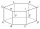 The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees.
The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - Velocity ratio
 Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui - Inscribed circle
 Write the equation of an incircle of the triangle KLM if K [2,1], L [6,4], M [6,1].
Write the equation of an incircle of the triangle KLM if K [2,1], L [6,4], M [6,1]. - Northeasterly 9681
 A military unit marches in a northerly direction from point A to point B, 15 km away. From place B, it goes 12 km in a northeasterly direction to place C. Determine the direct distance of cities A and C and certainly the deviation -alpha- by which the uni
A military unit marches in a northerly direction from point A to point B, 15 km away. From place B, it goes 12 km in a northeasterly direction to place C. Determine the direct distance of cities A and C and certainly the deviation -alpha- by which the uni - Scale
 The student drew the cylinder in scale 7:1. How many times is the volume of the cylinder smaller in reality?
The student drew the cylinder in scale 7:1. How many times is the volume of the cylinder smaller in reality? - Maturitný - RR - base
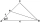 In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places.
In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places. - Directional 2595
 Calculate the interior angles of triangle ABC using vectors. Coordinates A [2; 4] B [4; 6] C [0; -4]. Calculate directional vectors of sides, parametric and general equations of sides, parametric and general equations of lines, calculate area, calculate h
Calculate the interior angles of triangle ABC using vectors. Coordinates A [2; 4] B [4; 6] C [0; -4]. Calculate directional vectors of sides, parametric and general equations of sides, parametric and general equations of lines, calculate area, calculate h - Perpendicular and parallel
 Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines?
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Octahedron - sum
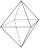 On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al
On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Tunnel - quadrilateral
 How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral.
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - Mast angles and height
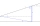 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Airplane navigation
 An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)?
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)? - Angle
 A straight line p given by the equation y = (-8)/(3) x (+)76. Calculate the size of the angle in degrees between line p and y-axis.
A straight line p given by the equation y = (-8)/(3) x (+)76. Calculate the size of the angle in degrees between line p and y-axis. - Scalar dot product
 Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120°
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - Area and two angles
 Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Height of poplar
 From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar.
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar. - Approximation of tangent fx
 What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°.
What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°. - Tangens parallelogram
 If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4)
If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4) - V-belt
 Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes)
Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes)
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
