Geometry - math word problems - page 155 of 162
Number of problems found: 3232
- A boy
A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Perpendicular 5865
We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube? - An observer
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - Quadrilateral - irregular
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Isosceles 7661
The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles. - Parametrically 6400
Find the angle of the line, which is determined parametrically x = 5 + t y = 1 + 3t z = -2t t belongs to R and the plane, which is determined by the general equation 2x-y + 3z-4 = 0. - Unit circle
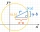In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - Length of the chord
Calculate the length of the chord in a circle with a radius of 25 cm and a central angle of 26°. - Space vectors 3D
The vectors u = (1; 3;- 4) and v = (0; 1; 1) are given. Find their sizes, calculate their angles, and determine the distances between them. - Float boya
A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³. - Cuboids
Two separate cuboids with different orientations are in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633) - Water channel
The cross-section of the water channel is a trapezoid. The bottom width is 19.7 m, the water surface width is 28.5 m, and the side walls have a slope of 67°30' and 61°15'. Calculate how much water flows through the channel in 5 minutes if the water flows - Rhombus
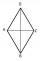ABCD is a rhombus, ABD is an equilateral triangle, and AC is equal to 4. Find the area of the rhombus. - Slope
What is the slope of a line with an inclination -325°? - Angle between vectors
Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21) - Geodesist
Triangle-shaped field (triangle ABC) has a side AB = 129 m. path XY is parallel to the side AB, which divides triangle ABC into two parts with the same area. What will be the length of path XY? Help, please, geodesist. - Three vertices
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Two forces
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer. - Decide 2
Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
