Geometry - math word problems - page 72 of 162
Number of problems found: 3238
- Right triangular prism
 We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area
We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area - Cuboid height
 What is the cuboid's height if its base edges are 15 cm and 4 cm long and its volume is 420 cm cubic?
What is the cuboid's height if its base edges are 15 cm and 4 cm long and its volume is 420 cm cubic? - Measuring cylinder
 A measuring cylinder has a base radius of 35mm and a height of 500mm. Calculate the surface area wetted by the liquid if the level reaches a height of 35cm.
A measuring cylinder has a base radius of 35mm and a height of 500mm. Calculate the surface area wetted by the liquid if the level reaches a height of 35cm. - Tetrahedron 82497
 The sum of the lengths of all the edges of the regular tetrahedron ABCD is 48 cm. How many cm is the segment XY if you know that X is AB's midpoint and Y is CD's midpoint?
The sum of the lengths of all the edges of the regular tetrahedron ABCD is 48 cm. How many cm is the segment XY if you know that X is AB's midpoint and Y is CD's midpoint? - The raft
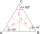 The raft for washing beets has the shape of a prism with the base of an isosceles triangle, the base of which is 6.8 m (width of the raft) and a height of 4.8 m (depth of the raft, height of the triangle). The raft is 35 m long (prism height). Calculate t
The raft for washing beets has the shape of a prism with the base of an isosceles triangle, the base of which is 6.8 m (width of the raft) and a height of 4.8 m (depth of the raft, height of the triangle). The raft is 35 m long (prism height). Calculate t - Half-cylinder-shaped 31491
 How many cubic meters of air is in an empty half-cylinder-shaped aircraft hangar if the hall is 30 m long and 12 m high at the highest point?
How many cubic meters of air is in an empty half-cylinder-shaped aircraft hangar if the hall is 30 m long and 12 m high at the highest point? - Perpendiculars 17003
 What is the hole volume drilled by the drill in the shape of a right triangle that revolves around a longer perpendicular? The perpendiculars of the triangle are 10 cm and 3 cm long.
What is the hole volume drilled by the drill in the shape of a right triangle that revolves around a longer perpendicular? The perpendiculars of the triangle are 10 cm and 3 cm long. - Length 6235
 Length 25m, width 10m, depth 160 cm. How many square meters are needed to line the pool?
Length 25m, width 10m, depth 160 cm. How many square meters are needed to line the pool? - Cone
 The circular cone of height 14 cm and volume 4396 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut.
The circular cone of height 14 cm and volume 4396 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut. - Cylinder 46101
 Barell has a cylinder shape, a volume of 130 l, and a base radius of 30 cm. What is the height of the barrel?
Barell has a cylinder shape, a volume of 130 l, and a base radius of 30 cm. What is the height of the barrel? - A sphere
 A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and
A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and - Cone - side
 If the cone's height is 125 mm and its side length is 17 cm, find its surface area and volume.
If the cone's height is 125 mm and its side length is 17 cm, find its surface area and volume. - Fire tank
 1428 hl of water is filled in a block-shaped fire tank with the edges of the base 12 m and 7 m. Calculate the area of water-wetted areas.
1428 hl of water is filled in a block-shaped fire tank with the edges of the base 12 m and 7 m. Calculate the area of water-wetted areas. - Distance of lines
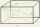 Find the distance of lines AE and CG in cuboid ABCDEFGH if given | AB | = 3cm, | AD | = 2 cm, | AE | = 4cm
Find the distance of lines AE and CG in cuboid ABCDEFGH if given | AB | = 3cm, | AD | = 2 cm, | AE | = 4cm - Glass aquarium
 How many m² of glass are needed to produce an aquarium with a bottom dimension of 70 cm x 40 cm and a height of 50 cm?
How many m² of glass are needed to produce an aquarium with a bottom dimension of 70 cm x 40 cm and a height of 50 cm? - Surface and volume od cuboid
 The square base of the cuboid has an area of Sp = 36 cm2, and its height is 80 mm. Determine its surface area and volume.
The square base of the cuboid has an area of Sp = 36 cm2, and its height is 80 mm. Determine its surface area and volume. - Triangular prism
 The perpendicular triangular prism is a right triangle with a 5 cm leg. The prism's largest wall area is 130 cm2, and the body height is 10 cm. Calculate the body volume.
The perpendicular triangular prism is a right triangle with a 5 cm leg. The prism's largest wall area is 130 cm2, and the body height is 10 cm. Calculate the body volume. - Rotating cone
 Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm.
Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm. - 3s prism
 A regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm is given. Calculate the prism's volume.
A regular perpendicular triangular prism with a height of 19.0 cm and a base edge of 7.1 cm is given. Calculate the prism's volume. - Cuboid box
 How much m² paper is needed for the sticking cuboid box of dimensions 50 cm, 40 cm, and 30 cm? To the folds, add one-tenth the area.
How much m² paper is needed for the sticking cuboid box of dimensions 50 cm, 40 cm, and 30 cm? To the folds, add one-tenth the area.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
