Geometry - math word problems - page 12 of 162
Number of problems found: 3238
- Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - The amphitheater
 The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle?
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Geometric 34741
 What geometric shape do all points in the plane have the same distance from a given point in the plane?
What geometric shape do all points in the plane have the same distance from a given point in the plane? - Clock face
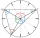 On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles.
On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Three points
 Three points, K (-3; 2), L (-1; 4), and M (3, -4), are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write
Three points, K (-3; 2), L (-1; 4), and M (3, -4), are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write - The chord
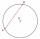 A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - The bridge
 Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen sees the bridge from the largest angle?
Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen sees the bridge from the largest angle? - Coefficient 4872
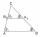 Find out if the triangles ABC and A'B'C' are similar, determine the similarity coefficient and write the similarity: a = 40 mm, b = 48 mm, c = 32 mm a´ = 60 mm, b´ = 50 mm, c´ = 40 mm
Find out if the triangles ABC and A'B'C' are similar, determine the similarity coefficient and write the similarity: a = 40 mm, b = 48 mm, c = 32 mm a´ = 60 mm, b´ = 50 mm, c´ = 40 mm - Isosceles 67744
 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Determine 44221
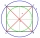 For circles k1 (S1, 4cm) and k2 (S2, 3cm) and it holds that | S1S2 | = 8cm. Determine the distance between the circles K1 and K2.
For circles k1 (S1, 4cm) and k2 (S2, 3cm) and it holds that | S1S2 | = 8cm. Determine the distance between the circles K1 and K2. - The coordinates
 The coordinates (5, 2) and (-6, 2) are vertices of a hexagon. Explain how to find the length of the segment formed by these endpoints. How long is the segment?
The coordinates (5, 2) and (-6, 2) are vertices of a hexagon. Explain how to find the length of the segment formed by these endpoints. How long is the segment? - Parametric form
 Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation. - Applies 14683
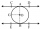 Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC?
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - Determine
 Determine which type of quadrilateral ABCD is and find its perimeter if you know the coordinates of vertices: A/2,4 /, B / -2,1 /, C / -2, -2 /, D/2, -5 /.
Determine which type of quadrilateral ABCD is and find its perimeter if you know the coordinates of vertices: A/2,4 /, B / -2,1 /, C / -2, -2 /, D/2, -5 /. - Spectators 7562
 The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle?
The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle? - Similar triangles
 We have similar triangles ABC with angle CAB=45° and angle ACB= 30° and a similar triangle OPN. What is the angle NOP in a similar triangle?
We have similar triangles ABC with angle CAB=45° and angle ACB= 30° and a similar triangle OPN. What is the angle NOP in a similar triangle? - Determine 80754
 The perimeter of triangle MAK is 216 mm, side a = 81 mm, and side k = 62 mm. Determine the side length of the triangle OSA if the triangle MAK is congruent to the triangle OSA.
The perimeter of triangle MAK is 216 mm, side a = 81 mm, and side k = 62 mm. Determine the side length of the triangle OSA if the triangle MAK is congruent to the triangle OSA. - Two angles
 The triangles ABC and A'B'C 'are similar. In the ABC triangle, the two angles are 25° and 65°. Explain why in the triangle A'B'C 'is the sum of two angles of 90 degrees.
The triangles ABC and A'B'C 'are similar. In the ABC triangle, the two angles are 25° and 65°. Explain why in the triangle A'B'C 'is the sum of two angles of 90 degrees. - Four sides of trapezoid
 The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area.
The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area. - Right-angled triangle
 Determine point C so that triangle ABC is right-angled and isosceles with hypotenuse AB, where A[4,-6], B[-2,10]
Determine point C so that triangle ABC is right-angled and isosceles with hypotenuse AB, where A[4,-6], B[-2,10]
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
