Planimetrics - math word problems - page 178 of 185
Number of problems found: 3686
- Mast angles and height
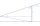 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Mast
 The mast has 16 a long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 9.7°. Determine the height of the mast if the sun above the horizon is at an angle 40°48'.
The mast has 16 a long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 9.7°. Determine the height of the mast if the sun above the horizon is at an angle 40°48'. - Airplane navigation
 An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)?
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)? - Third roots
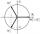 Determine the sum of the three complex third roots of the number 64 .
Determine the sum of the three complex third roots of the number 64 . - Difference 83079
 On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road?
On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road? - Quadrilateral 81097
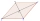 The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Regular octagon pad
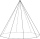 You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - Modulus and argument
 Find the mod z and argument z if z=i
Find the mod z and argument z if z=i - Angle
 A straight line p given by the equation y = (-8)/(3) x (+)76. Calculate the size of the angle in degrees between line p and y-axis.
A straight line p given by the equation y = (-8)/(3) x (+)76. Calculate the size of the angle in degrees between line p and y-axis. - Area and two angles
 Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Height of poplar
 From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar.
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50°10' and the bottom of the poplar at a depth angle of 58°. Calculate the height of the poplar. - Approximation of tangent fx
 What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°.
What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°. - Tangens parallelogram
 If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4)
If ∠BAD between the sides AB and AD of the parallelogram is θ, what is tan θ? See diagram: A=(7,1) B=(5,-2) C=(12,1) D=(14,4) - V-belt
 Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes)
Calculate the length of the V-belt when the diameter of the pulleys is: D1 = 600 mm D2 = 120 mm d = 480 mm (distance between pulley axes) - An observer
 An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower?
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - A boy
 A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff.
A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Complex square roots
 Determine the sum of the three square roots of 343.
Determine the sum of the three square roots of 343. - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
