Pythagorean theorem - math word problems - page 48 of 73
Number of problems found: 1451
- Square side
 Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0.
Calculate the length of the side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0. - Circumscribing
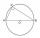 Find the radius of the circumscribed circle to the right triangle with legs 6 cm and 3 cm.
Find the radius of the circumscribed circle to the right triangle with legs 6 cm and 3 cm. - Equation of the circle
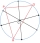 Find an equation of the circle whose diameter has endpoints (1,-4) and (3,2).
Find an equation of the circle whose diameter has endpoints (1,-4) and (3,2). - Vectors abs sum diff
 The vectors a = (4,2), b = (- 2,1) are given. Calculate: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|.
The vectors a = (4,2), b = (- 2,1) are given. Calculate: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|. - Distance between 2 points
 Find the distance between the points (7, -9), (-1, -9)
Find the distance between the points (7, -9), (-1, -9) - Equation of a circle
 Write the general equation of a circle with center S(2;5) and point B(5;6) lying on this circle.
Write the general equation of a circle with center S(2;5) and point B(5;6) lying on this circle. - Center
 Calculate the coordinates of the circle center: x² -10x + y² +9 = 0
Calculate the coordinates of the circle center: x² -10x + y² +9 = 0 - Height
 Is it true that the height is less or equal to half of the hypotenuse in any right triangle?
Is it true that the height is less or equal to half of the hypotenuse in any right triangle? - Distance problem 2
 A=(x,2x) B=(2x,1) Distance AB=√2, find the value of x
A=(x,2x) B=(2x,1) Distance AB=√2, find the value of x - Vector 7
 Given vector OA(12,16) and vector OB(4,1). Find vector AB and vector |A|.
Given vector OA(12,16) and vector OB(4,1). Find vector AB and vector |A|. - Equilateral cone
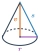 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Pentagonal pyramid
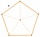 Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm. - Top of the tower
 The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Pit
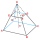 The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n
The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n - Spherical cap
 What is the surface area of a spherical cap, the base diameter 27 m, and height 2 m?
What is the surface area of a spherical cap, the base diameter 27 m, and height 2 m? - A cylinder
 A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm?
A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm? - Wooden 3
 A wooden board 2.5 m long has a cross-section in the shape of a regular trapezoid whose parallel sides have lengths of 1.2 dm and 8 cm. The height of the trapezoid is 3 cm. Calculate: a) the surface area of the board to calculate the consumption of stai
A wooden board 2.5 m long has a cross-section in the shape of a regular trapezoid whose parallel sides have lengths of 1.2 dm and 8 cm. The height of the trapezoid is 3 cm. Calculate: a) the surface area of the board to calculate the consumption of stai - The base 2
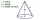 The base diameter of a right cone is 16cm, and its slant height is 12cm. A. ) Find the perpendicular height of the cone to 1 decimal place. B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14
The base diameter of a right cone is 16cm, and its slant height is 12cm. A. ) Find the perpendicular height of the cone to 1 decimal place. B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14 - Billiard balls
 A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original.
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original. - MO SK/CZ Z9–I–3
 John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
