Ratio + circle - practice problems
Number of problems found: 62
- Revolutions 83126
 The tractor's rear wheel has a diameter of 1.6 m, and the front wheel is 96 cm. What ratio are the numbers of their revolutions? How many times does the front wheel turn, and how many times does the rear wheel turn on a track 1942 m long?
The tractor's rear wheel has a diameter of 1.6 m, and the front wheel is 96 cm. What ratio are the numbers of their revolutions? How many times does the front wheel turn, and how many times does the rear wheel turn on a track 1942 m long? - Coordinate 82855
 What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system?
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - Describes 82518
 The minute hand describes an angle of 180 degrees in half an hour. In how many minutes does the minute hand cover an angle of 192 degrees?
The minute hand describes an angle of 180 degrees in half an hour. In how many minutes does the minute hand cover an angle of 192 degrees? - Dimensions 82414
 The flag of Brazil has a yellow diamond on a green field with a blue circle inside. If we had a flag with dimensions of 70 cm x 50 cm, the rhombus would have a side 35 cm long and a height of 30 cm. Indicate with fractions in basic form what part of the f
The flag of Brazil has a yellow diamond on a green field with a blue circle inside. If we had a flag with dimensions of 70 cm x 50 cm, the rhombus would have a side 35 cm long and a height of 30 cm. Indicate with fractions in basic form what part of the f
- Magnitudes 80788
 The minute hand is three times longer than the second hand. In what ratio are the magnitudes of the velocities of their endpoints?
The minute hand is three times longer than the second hand. In what ratio are the magnitudes of the velocities of their endpoints? - Calculate 70814
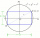 The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle. - Circumference 69934
 You know the ratio of the circumference of the circle to the area is 4:9. What is the circle's diameter?
You know the ratio of the circumference of the circle to the area is 4:9. What is the circle's diameter? - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - The ratio
 The ratio of the lengths of the two circles is 5:2. Find the ratio of a a) the radii of these circles b) the areas for these circles
The ratio of the lengths of the two circles is 5:2. Find the ratio of a a) the radii of these circles b) the areas for these circles
- Quadrilateral in circle
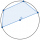 A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles.
A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles. - Megapizza
 Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion?
Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion? - Gears
 The front gear on the bike has 32 teeth, and the rear wheel has 12 teeth. How many times does the bike's rear-wheel turn if you turn the right pedal 30 times? What distance will you go if the circumference of the bicycle wheel is 250 cm?
The front gear on the bike has 32 teeth, and the rear wheel has 12 teeth. How many times does the bike's rear-wheel turn if you turn the right pedal 30 times? What distance will you go if the circumference of the bicycle wheel is 250 cm? - Sphere in cone
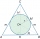 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Ratio of squares
 A circle is given in which a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
A circle is given in which a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
- Diameters: 23901
 When paying, we use euro coins with the following diameters: The 10-cent coin has a diameter of 19.75 mm. The 20-cent coin has a diameter of 22.25 mm. The 50-cent coin has a diameter of 24.25 mm. Find out in what ratio the diameters of these coins are.
When paying, we use euro coins with the following diameters: The 10-cent coin has a diameter of 19.75 mm. The 20-cent coin has a diameter of 22.25 mm. The 50-cent coin has a diameter of 24.25 mm. Find out in what ratio the diameters of these coins are. - Construct 13581
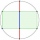 The vertices of the triangle ABC lie on the circle k. The circle k is divided into three parts in a ratio of 1:2:3. Construct this triangle.
The vertices of the triangle ABC lie on the circle k. The circle k is divided into three parts in a ratio of 1:2:3. Construct this triangle. - Minutes 13551
 What is the angle of the clock hands: a / at 16 hours 15 minutes b / v 8 hours and 4 minutes
What is the angle of the clock hands: a / at 16 hours 15 minutes b / v 8 hours and 4 minutes - Calculate 12061
 The area of the two circles is in a 4:9 ratio. The larger circle has a diameter of 18 cm. Calculate the radius of the smaller circle.
The area of the two circles is in a 4:9 ratio. The larger circle has a diameter of 18 cm. Calculate the radius of the smaller circle. - Ratio of volumes
 If the heights of two cylindrical drums are in the ratio 7:8 and their base radii are in the ratio 4:3. What is the ratio of their volumes?
If the heights of two cylindrical drums are in the ratio 7:8 and their base radii are in the ratio 4:3. What is the ratio of their volumes?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
