Triangle practice problems - page 67 of 126
Number of problems found: 2501
- Triangular prism,
 The regular triangular prism, whose edges are identical, has a surface of 2514 cm² (square). Find the volume of this body in cm³ (l).
The regular triangular prism, whose edges are identical, has a surface of 2514 cm² (square). Find the volume of this body in cm³ (l). - Calculate 6706
 Given a triangle KLM points K [-3.2] L [7, -3] M [8.5]. Calculate the side lengths and perimeter.
Given a triangle KLM points K [-3.2] L [7, -3] M [8.5]. Calculate the side lengths and perimeter. - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Triangle
 Calculate the area of the triangle ABC if b = c = 17 cm, R = 19 cm (R is the circumradius).
Calculate the area of the triangle ABC if b = c = 17 cm, R = 19 cm (R is the circumradius). - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - 3 positive charges
 Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos
Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos - Prism - eq triangle
 Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm.
Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm. - Cross-section 47131
 The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume
The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume - Central park in city
 The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou
The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou - Isosceles 2588
 Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Height of the arc - formula
 Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this?
Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this? - Isosceles weight
 A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight?
A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight? - Space diagonal angles
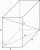 Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD.
Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Rectangular 4624
 The lengths of the sides of the rectangular garden are in the ratio of 1:2. The junction of the centers of adjacent sides is 20 m long. Calculate the perimeter and acreage of the land.
The lengths of the sides of the rectangular garden are in the ratio of 1:2. The junction of the centers of adjacent sides is 20 m long. Calculate the perimeter and acreage of the land. - Angle of diagonals
 Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°.
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°. - RT - inscribed circle
 In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle.
In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle. - Tetrahedral pyramid
 Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - Right triangular prism
 We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area
We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area - Coordinates 59863
 The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO
The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO - Rectangle
 There is a rectangle with a length of 12 cm and a diagonal 8 cm longer than the width. Calculate the area of a rectangle.
There is a rectangle with a length of 12 cm and a diagonal 8 cm longer than the width. Calculate the area of a rectangle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
