Volume + quadratic equation - practice problems
Number of problems found: 59
- Centimeters 82996
 The volume of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Determine the height of the trapezoid in centimeters.
The volume of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Determine the height of the trapezoid in centimeters. - Right-angled 82416
 What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²?
What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²? - Quadrilateral 81033
 The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases.
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases. - Parabolic 79764
 In a tennis match, Adrien is 5 m from the net when he hits a ball 80 cm off the ground. The maximum height of its parabolic path passing through the net was 1.5 m. If the length of the court is 23.77 m, will the ball land inside the court?
In a tennis match, Adrien is 5 m from the net when he hits a ball 80 cm off the ground. The maximum height of its parabolic path passing through the net was 1.5 m. If the length of the court is 23.77 m, will the ball land inside the court?
- A cuboid 2
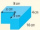 A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199. Calculate the value of x.
A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199. Calculate the value of x. - Determine 73454
 The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm.
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Vertically 65984
 We threw the stone vertically upwards at a speed of v = 15m. s-1. How long will it be at a) 10 m, b) 12 m?
We threw the stone vertically upwards at a speed of v = 15m. s-1. How long will it be at a) 10 m, b) 12 m? - Magnitudes 64704
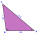 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
- Assembling 63964
 Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit?
Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit? - Calculate 62864
 The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides.
The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides. - Side wall planes
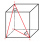 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - The surface
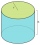 The surface of the cylinder is 1570 cm²; its height is 15 cm. Find the volume and radius of the base.
The surface of the cylinder is 1570 cm²; its height is 15 cm. Find the volume and radius of the base. - Truncated pyramid
 The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
- The block
 The block, the edges formed by three consecutive GP members, has a surface area of 112 cm². The sum of the edges that pass through one vertex is 14 cm. Calculate the volume of this block.
The block, the edges formed by three consecutive GP members, has a surface area of 112 cm². The sum of the edges that pass through one vertex is 14 cm. Calculate the volume of this block. - Consider
 Consider all square prisms with a height of 10 cm. If x is the measurement of the base edge in cm, and y is the prism's volume in cm³. Graph the function
Consider all square prisms with a height of 10 cm. If x is the measurement of the base edge in cm, and y is the prism's volume in cm³. Graph the function - The cylinder
 In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder.
In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder. - Rotary cylinder
 In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.
In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height. - Hard cone problem
 The cone's surface is 200 cm², and its height is 7 centimeters. Calculate the volume of this cone.
The cone's surface is 200 cm², and its height is 7 centimeters. Calculate the volume of this cone.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
