Pytagorova veta - slovné úlohy a príklady - strana 22 z 73
Počet nájdených príkladov: 1444
- Záhrada 17
 Záhrada má tvar pravouhlého trojuholníka s rozlohou 96 metrov štvorcových a jednou odvesnou dlhou 16 m. Koľko metrov pletiva treba na jej oplotenie?
Záhrada má tvar pravouhlého trojuholníka s rozlohou 96 metrov štvorcových a jednou odvesnou dlhou 16 m. Koľko metrov pletiva treba na jej oplotenie? - RR lichobežník
 V rovnoramennom lichobežníku ABCD má rameno dĺžku 5,2 cm, stredná priečka má dĺžku 7 cm a výška sa rovná 4,8 cm. Vypočítajte dĺžky oboch základní.
V rovnoramennom lichobežníku ABCD má rameno dĺžku 5,2 cm, stredná priečka má dĺžku 7 cm a výška sa rovná 4,8 cm. Vypočítajte dĺžky oboch základní. - Kvetinový záhon
 Kvetinový záhon má tvar kosoštvorca so stranou a = 35 dm. Dlhšia uhlopriečka je dlhá 56 dm. Vypočítajte obsah kvetinového záhonu.
Kvetinový záhon má tvar kosoštvorca so stranou a = 35 dm. Dlhšia uhlopriečka je dlhá 56 dm. Vypočítajte obsah kvetinového záhonu. - PT trojuholníky
 Koľko pravouhlých trojuholníkov môžeme zostrojiť z úsečiek dlhých 3,4,5,6,8,10,12,13,15,17 cm? (Nezabudni na trojuholníkovú nerovnosť).
Koľko pravouhlých trojuholníkov môžeme zostrojiť z úsečiek dlhých 3,4,5,6,8,10,12,13,15,17 cm? (Nezabudni na trojuholníkovú nerovnosť). - PT odvesna a obvod
 Vypočítajte dĺžky strán pravouhlého trojuholníka ABC s preponou c, ak dĺžka odvesny a=84 a obvod trojuholníka o=279.
Vypočítajte dĺžky strán pravouhlého trojuholníka ABC s preponou c, ak dĺžka odvesny a=84 a obvod trojuholníka o=279. - Tetiva 2
 Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k.
Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k. - Cestný násyp
 Cestný násyp má priečny rez tvaru rovnoramenného lichobežníka o základniach 8 metrov a 13 metrov, ramená dĺžky 3 metrov. Koľko metrov kubických zeminy je v násype o dĺžke 986 metrov?
Cestný násyp má priečny rez tvaru rovnoramenného lichobežníka o základniach 8 metrov a 13 metrov, ramená dĺžky 3 metrov. Koľko metrov kubických zeminy je v násype o dĺžke 986 metrov? - RR lichobežník
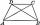 Vypočítaj dĺžku uhlopriečky a výšky rovnoramenného lichobežníka ABCD, ktorého základne majú dĺžky a = |AB| = 37 cm, c = |CD| = 29 cm a ramená b = d = |BC| = |AD| = 28 cm.
Vypočítaj dĺžku uhlopriečky a výšky rovnoramenného lichobežníka ABCD, ktorého základne majú dĺžky a = |AB| = 37 cm, c = |CD| = 29 cm a ramená b = d = |BC| = |AD| = 28 cm. - Zväčšenie štvorca
 Ak zväčšime stranu štvorca, zväčší sa aj jeho obsah o 40 %. O koľko percent sa zväčšila jeho strana?
Ak zväčšime stranu štvorca, zväčší sa aj jeho obsah o 40 %. O koľko percent sa zväčšila jeho strana? - Priemer kmeňu
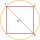 Aký najmenší priemer musí mať kmeň stromu, aby sme z neho mohli vyrezať hranoliek so štvorcovým prierezom s dĺžkou strany 20 cm?
Aký najmenší priemer musí mať kmeň stromu, aby sme z neho mohli vyrezať hranoliek so štvorcovým prierezom s dĺžkou strany 20 cm? - Strana
 Vypočítajte veľkosť strany štvorca ABCD s vrcholom A[0, 0], ak uhlopriečka BD leží na priamke p: -4x -5 =0.
Vypočítajte veľkosť strany štvorca ABCD s vrcholom A[0, 0], ak uhlopriečka BD leží na priamke p: -4x -5 =0. - Súčet 14
 Súčet štvorcov nad stranami pravoúhleho trojuholníka je 900 cm². Vypočítaj aký je obsah štvorca nad preponou tohto trojuholníka!
Súčet štvorcov nad stranami pravoúhleho trojuholníka je 900 cm². Vypočítaj aký je obsah štvorca nad preponou tohto trojuholníka! - Zábradlie schodiska
 Zistite, či bude zábradlie pri schodisku s 20 schodmi dlhšie ako 7 m, ak je schod 32 cm široký a 15 cm vysoký. (1=Áno, 0 = Nie)
Zistite, či bude zábradlie pri schodisku s 20 schodmi dlhšie ako 7 m, ak je schod 32 cm široký a 15 cm vysoký. (1=Áno, 0 = Nie) - ABCD - kosoštvorec
 V kosoštvorci ABCD je uhlopriečka e = 24 cm a veľkosť uhla SAB je 28 stupňov, kde S je průsečnik uhlopriečok. Vypočítaj obvod kosoštvorca.
V kosoštvorci ABCD je uhlopriečka e = 24 cm a veľkosť uhla SAB je 28 stupňov, kde S je průsečnik uhlopriečok. Vypočítaj obvod kosoštvorca. - Rebrík o stenu
 O budovu sa opiera rebrík, jeho dĺžka je 7,5 metrov. Dole je vzdialený od budovy 2 metre. V akej výške sa opiera o stenu?
O budovu sa opiera rebrík, jeho dĺžka je 7,5 metrov. Dole je vzdialený od budovy 2 metre. V akej výške sa opiera o stenu? - Stredné priečky 2
 Vypočítaj dĺžku stredných priečok v rovnoramennom trojuholníku, ak dĺžka ramena je 52mm a výška na základnú má 48mm
Vypočítaj dĺžku stredných priečok v rovnoramennom trojuholníku, ak dĺžka ramena je 52mm a výška na základnú má 48mm - Trať - klesanie
 Vypočítaj klesanie železničnej trate v úseku 7,2 km o 21,6 m v promile.
Vypočítaj klesanie železničnej trate v úseku 7,2 km o 21,6 m v promile. - Dĺžka uhlopriečky
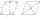 Nájdite dĺžku uhlopriečky AC kosoštvorca ABCD, ak jeho obvod P = 112 dm a druhá uhlopriečka BD má dĺžku 36 dm.
Nájdite dĺžku uhlopriečky AC kosoštvorca ABCD, ak jeho obvod P = 112 dm a druhá uhlopriečka BD má dĺžku 36 dm. - Rebrík - M
 Michael má o bok svojho domu opretý 35 stôp dlhý rebrík. Ak je spodná časť rebríka vzdialená 21 stôp od jeho domu, koľko stôp nad zemou sa rebrík dotýka domu?
Michael má o bok svojho domu opretý 35 stôp dlhý rebrík. Ak je spodná časť rebríka vzdialená 21 stôp od jeho domu, koľko stôp nad zemou sa rebrík dotýka domu? - Kolmý priemet
 Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0.
Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0.
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
