Částice
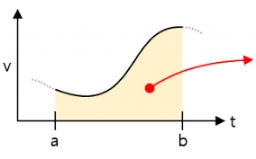
Částice se pohybuje v přímce tak, že její rychlost (m/s) v čase t sekund je dána v (t) = 3t2-4t-4, t > 0.
Zpočátku je částice 8 metrů vpravo od pevného původu.
Po kolika sekundách je částice na počátku?
Vaše odpověď:
Zpočátku je částice 8 metrů vpravo od pevného původu.
Po kolika sekundách je částice na počátku?
Vaše odpověď:
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
základní operace a pojmyJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Běžec 3
Běžec dosáhne rychlosti 30 km/h po 3 sekundách od startu. Určete jeho zrychlení. - Volný pád Penny
Muž shodil cent z vrcholu 500 metrů vysoké budovy. Po t sekundách cent klesl o vzdálenost s metrů, kde s(t)=500-5t² . Určete průměrnou rychlost mezi 1 s a 5 s. - Skatepark FO
Lucka vyrazila odpoledne do skateparku. Při sjíždění dolů z jednoduché překážky měla na počátku v čase t0 = 0 s rychlost v0 = 0,6 m/s a každou sekundu pohybu se její velikost zvětšila o 0,2 m/s. Po 3 s zrychleného pohybu Lucka pokračovala po rovině rovnom - Délka eskalátoru
Eskalator v podchodu metra se pohybuje rychlostí 0,7 m/s. Určí jeho délku pokud od nastoupení do vystoupení cestujícího uplyne čas 62,3 s - Polohový vektor hmotného bodu 2
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2 - Polohový vektor hmotného bodu
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t - Úhlové zrýchlení
Částice se začala pohybovat z klidu po kružnici konstantním úhlovým zrychlením. Po pěti obězích (n = 5) její úhlová rychlost dosáhla hodnotu ω = 12 rad/s . Vypočtěte velikost úhlového zrychlení ε tohoto pohybu a časový interval potřebný na prvních 5 oběhů
