Ornament
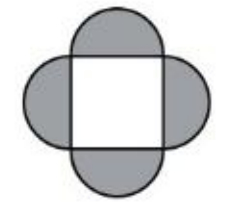
Ornament je složen z jednoho čtverce a čtyř tmavých půlkruhů. Obsah čtverce je 4 cm2. Vypočítejte obsah jednoho tmavého půlkruhu a výsledek zaokrouhlete na setiny.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Chcete zaokrouhlit číslo?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikaplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Obsah čtverců
Vypočítejte obsah čtverce a výsledek zaokrouhlete na decimetry čtvereční. a) a = 1,52 dm b) a = 13 268 mm c) a = 562 cm d) a = 1,52 m - Osový řez válce
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - Kruhová výseč 2
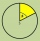Vypočítejte obsah kruhové výseče dané úhlem 220 stupňů, je li poloměr kruhu 20 cm. Výsledek zaokrouhlete na cm2 - Erb
Třída si vytvořila vlastní erb, který měl tvar složený z rovnoramenného lichoběžníku ABCD (kratší základna je dlouhá a=4,5 cm, delší 2a=9 cm, výška lichoběžníku 6 cm) a půlkruhu se středem S a průměrem AB. Lichoběžník tvořily tři shodné rovnoramenné trojú - Obrazec
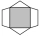Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Obsah rovnoramenného lichoběžníku
Vypočítej obsah rovnoramenného lichoběžníku ABCD, jehož delší základna měří 48 cm, kratší základna měří 3/4 z delší a rameno lichoběžníku měří 2/3 z delší základny. Výsledek zaokrouhlí na setiny. - Srdce
Stylizovaný tvar srdce vznikl ze čtverce o straně 5 cm a dvou půlkruhů nad jeho stranami. Vypočítej obsah a obvod.
