Příklady pro výpočet plošného obsahu tělesa (povrchu tělesa) - strana 14 z 50
Počet nalezených příkladů: 989
- Hluboký bazén
Kolik litrů vody je třeba napustit do bazénu, který je 25m dlouhý, 800cm široký a 20dm hluboký. Bazén má být naplněn do 3/4 jeho hloubky. Kolik eur zaplatíte za obklad bazénu ak m² obkladu stojí 20 eur? - Kruhový výsek
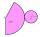Plášť kužele s poloměrem podstavy 20 cm a výškou 50 cm se rozvine do kruhového výseku. Jak velký je středový úhel tohoto výseku? - Krabice
Vypočítaj spotřebu papíru na krabici tvaru čtyřbokého hranolu s kosočtvercovou podstavou, podstavná hrana a=6cm, sousedící hrany svírá úhel alfa=60°. výška krabice je 10cm. Kolik m² papíru spotřebujeme na 100 takových krabic? - Plocha stanu
Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m. - Kolik
Kolik m² měděného plechu třeba na výměnu střechy věže kuželovitého tvaru, jejíž průměr je 13 metrů a výška 24 metrů, pokud na zahnutí a odpad počítáme 8% materiálu? - 1 kg cukru
1 kg kostkového cukru je tvořeno 840 krychlička o hraně 1,1 cm. Určete hustotu cukru a rozměr krabice jsou-li krychličky narovnány v sedmi řadách po devíti kostičkách. Kolik čtverečních metrů kartónu je třeba na výrobu 3000 těchto krabic? - Objem
Objem pravidelného čtyřbokého hranolu je 192 cm³. Velikost jeho podstavné hrany a tělesových výšky jsou v poměru 1:3. Vypočítejte povrch hranolu. - Koule 23
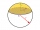Koule o průměru 20,6cm, řezem je kruh o průměru 16,2cm. .Jaký je objem výseče a povrch úseče? - Střecha
Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba? - Kulový odsek a výsek
Vypočtěte povrch kulového výseku, pokud kulový odsek, který je částí výseku, má poloměr podstavy ρ = 9 cm a výšku v = 2,4 cm. - Kvádr
Vypočtěte objem a povrch kvádru ABCDEFGH, jehož rozměry abc jsou v poměru 4:10:4, víte-li ze stenova úhlopříčka AC měří 46 cm a má od telesové úhlopříčky AG odchylku 55 stupňů. - Štvobokého 83259
Obvod štvobokého ihlava je 48 m a jeho výška je 2,5 m; kolik bude stát plech na tento jehlan, když 1 m² stojí 1,5 €; do plochy se počítá i 12% ztráta na spoje a záhyby. - Pravidelného 71484
Střecha věže má tvar pravidelného 4-bokého jehlanu a výškou 4m a hranou podstavy 6m. Zjistilo se, že je poškozeno 25% krytiny na střeše. Kolik metrů čtverečních krytiny je potřeba k opravě střechy? - Spotrebovalo 7910
Střecha rekreační chaty má tvar pravidelného čtyřbokého jehlanu o výšce 8m a podstavnou hranou 4m. Kolik ℅ připadlo na záhyby a spoje pokud se na pokrytí střechy spotřebovalo 75,9 metrů čtverečních plechu? - Počítačové 4994
Pan školník má vymalovat stěny počítačové učebny, jejíž délka je 7 m, šířka 5 m a výška 3 m. V učebně jsou čtyři čtvercová okna o délce 1 m; a dveře široké 1 m a vysoké 2 m. Nejméně koli kilogramu barvy má koupit, pokud 1 kg barvy utratí na 15 m²? - Střecha
2/3 plochy střechy ve tvaru pravidelného čtyřbokého jehlanu s hranou podstavy 9 m a výškou 6 m je už pokryta krytinou. Kolik třeba ještě pokrýt? - Střecha 7
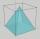Střecha má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou 12m a výškou 4m. Kolik procent připadlo na záhyby a odpad, jestliže se spotřebovalo na jeji zhotovení 181,4m² plechu? - Pravidelného 4905
Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90? - Čtyřboký hranol
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Stříška 2 Kolik plechu je třeba na stříšku, která má tvar pravidelného čtyřbokého jehlanu, jestliže její hrana je dlouhá 2,8 m a výška stříšky je 0,8 m. Počítej 10 % na překryv ( navíc).
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
