Přirozená čísla - slovní úlohy a příklady - strana 43 z 79
Počet nalezených příkladů: 1570
- Pravidelné skoky
 Zajíc se zúčastnil závodu dlouhých 2024 metrů. Ze startovní čáry se odrazil levou nohou a po celou dobu závodu pravidelně střídal levou, pravou a obě nohy. Když se zajíc odrazil levou nohou, skočil 35 dm, když se odrazil pravou nohou, skočil 15 dm, a když
Zajíc se zúčastnil závodu dlouhých 2024 metrů. Ze startovní čáry se odrazil levou nohou a po celou dobu závodu pravidelně střídal levou, pravou a obě nohy. Když se zajíc odrazil levou nohou, skočil 35 dm, když se odrazil pravou nohou, skočil 15 dm, a když - (čtverečních) 56801
 Máme vytvořit políčko ve tvaru obdélníku o rozloze 288 m² (čtverečních), tak aby strany byly celá čísla. Jaké jsou všechny rozměry obdélníkového políčka, které můžeme vytvořit? Kolik je řešení.
Máme vytvořit políčko ve tvaru obdélníku o rozloze 288 m² (čtverečních), tak aby strany byly celá čísla. Jaké jsou všechny rozměry obdélníkového políčka, které můžeme vytvořit? Kolik je řešení. - Ciferný součet 11
 Ciferný součet dvojciferního čísla Je 11. Po záměně pořadí číslic dostanu číslo, které je o 27 menší než myšlené číslo. Jaké číslo si myslím?
Ciferný součet dvojciferního čísla Je 11. Po záměně pořadí číslic dostanu číslo, které je o 27 menší než myšlené číslo. Jaké číslo si myslím? - Na kolik 2
 Na kolik největších čtvercových plechů rozřezal klempíř plást od rozměrech 16 dm a 96 dm?
Na kolik největších čtvercových plechů rozřezal klempíř plást od rozměrech 16 dm a 96 dm? - Z knihy
 Z knihy je vytržen 1 list. Součet čísel stránek všech zbývajících listů je 15 000. Jaká čísla měly stránky na listu, který byl z knihy vytržen?
Z knihy je vytržen 1 list. Součet čísel stránek všech zbývajících listů je 15 000. Jaká čísla měly stránky na listu, který byl z knihy vytržen? - Nejmenší 5464
 Zahrada je dlouhá 90m. Jaká nejmenší může být její šířka, lze-li projít (obvod) kroky 80 cm nebo 50 cm?
Zahrada je dlouhá 90m. Jaká nejmenší může být její šířka, lze-li projít (obvod) kroky 80 cm nebo 50 cm? - Vypočítejte 3818
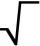 Máme 2 čísla. Kdybychom vynásobili třetí odmocninu prvního čísla s druhou odmocninou druhého čísla, dostali bychom číslo 18. Určete tato 2 čísla. Pokud má úloha v množině reálných čísel nekonečně mnoho řešení, vypočítejte jen celočíselné řešení.
Máme 2 čísla. Kdybychom vynásobili třetí odmocninu prvního čísla s druhou odmocninou druhého čísla, dostali bychom číslo 18. Určete tato 2 čísla. Pokud má úloha v množině reálných čísel nekonečně mnoho řešení, vypočítejte jen celočíselné řešení. - Zvonkohra
 Zvonkohra na nádvoří hraje v každou celou hodinu krátkou skladbu, a to počínaje 8. a konče 22. hodinou. Skladeb je celkem osmnáct, v celou hodinu se hraje vždy jen jedna a po odehrání všech osmnácti se začíná ve stejném pořadí znovu. Olga a Libor byli na
Zvonkohra na nádvoří hraje v každou celou hodinu krátkou skladbu, a to počínaje 8. a konče 22. hodinou. Skladeb je celkem osmnáct, v celou hodinu se hraje vždy jen jedna a po odehrání všech osmnácti se začíná ve stejném pořadí znovu. Olga a Libor byli na - Cena hrníčků a konvice
 Teta koupila 6 stejných hrníčků a jednu konvici na kávu. Celkem zaplatila 60 €. Konvice byla dražší než jeden hrníček, ale levnější než dva hrníčky. Teta si pamatovala, že všechny ceny byly v celých eurech. Kolik € stál jeden hrnek a kolik konvice?
Teta koupila 6 stejných hrníčků a jednu konvici na kávu. Celkem zaplatila 60 €. Konvice byla dražší než jeden hrníček, ale levnější než dva hrníčky. Teta si pamatovala, že všechny ceny byly v celých eurech. Kolik € stál jeden hrnek a kolik konvice? - Samopočet
 Samopočet funguje přesně jako kalkulačka. Hostinský chtěl na samopočte sečíst několik trojmístných přirozených čísel. Na první pokus dostal výsledek 2224. Pro kontrolu sečetl tato čísla znovu a vyšlo mu 2198. Proto sečetl tato čísla ještě jednou a nyní do
Samopočet funguje přesně jako kalkulačka. Hostinský chtěl na samopočte sečíst několik trojmístných přirozených čísel. Na první pokus dostal výsledek 2224. Pro kontrolu sečetl tato čísla znovu a vyšlo mu 2198. Proto sečetl tato čísla ještě jednou a nyní do - Z7–I–4 2018 MO Betka
 Karel si hrál s ozubenými koly, která byla sestavena do soukolí. Když zatočil jedním kolem, točila se všechna ostatní. První kolo mělo 32 a druhé 24 zubů. Když se třetí kolo otočilo (je uprostřed soukolí) přesně osmkrát, druhé kolo udělalo pět otáček a čá
Karel si hrál s ozubenými koly, která byla sestavena do soukolí. Když zatočil jedním kolem, točila se všechna ostatní. První kolo mělo 32 a druhé 24 zubů. Když se třetí kolo otočilo (je uprostřed soukolí) přesně osmkrát, druhé kolo udělalo pět otáček a čá - Potřebujeme 4402
 Naším úkolem je uložit obrázky tvaru obdélníku o rozměrech 105 mm a 42 mm tak, abychom zakryli nejmenší čtverec. Jaký bude jeho rozměr a kolik obrázků potřebujeme?
Naším úkolem je uložit obrázky tvaru obdélníku o rozměrech 105 mm a 42 mm tak, abychom zakryli nejmenší čtverec. Jaký bude jeho rozměr a kolik obrázků potřebujeme? - Kvíz
 V soutěži odpovídá 10 soutěžících na pět otázek, v každém kole na jednu otázku. Kdo odpoví správně, získá v daném kole tolik bodů, kolik soutěžících odpovědělo nesprávné. Jedna ze soutěžících po soutěži řekla: Celkově jsme získali 116 bodů, z toho já 30.
V soutěži odpovídá 10 soutěžících na pět otázek, v každém kole na jednu otázku. Kdo odpoví správně, získá v daném kole tolik bodů, kolik soutěžících odpovědělo nesprávné. Jedna ze soutěžících po soutěži řekla: Celkově jsme získali 116 bodů, z toho já 30. - V množině
 V množině N řešte danou rovnici: 1 – x + x² - x³ + x4 – x5 + …. + = 1/3
V množině N řešte danou rovnici: 1 – x + x² - x³ + x4 – x5 + …. + = 1/3 - Z7–I–5 MO 2018
 V zahradnictví Rose si jedna prodejna objednala celkem 120 růží v barvě červené a žluté, druhá prodejna celkem 105 růží v barvě červené a bílé a třetí prodejna celkem 45 růží v barvě žluté a bílé. Zahradnictví zakázku splnilo, a to tak, že růží stejné bar
V zahradnictví Rose si jedna prodejna objednala celkem 120 růží v barvě červené a žluté, druhá prodejna celkem 105 růží v barvě červené a bílé a třetí prodejna celkem 45 růží v barvě žluté a bílé. Zahradnictví zakázku splnilo, a to tak, že růží stejné bar - Převyšující 8196
 Abdul si vezme půjčku ve výši 200 000 od Ali a souhlasí se splacením v počtu splátek, přičemž každá splátka začíná 2. převyšující předchozí o 1 000, je-li první splátka 500, zjistěte, kolik splátek bude zapotřebí k úplnému vyplacení této půjčky?
Abdul si vezme půjčku ve výši 200 000 od Ali a souhlasí se splacením v počtu splátek, přičemž každá splátka začíná 2. převyšující předchozí o 1 000, je-li první splátka 500, zjistěte, kolik splátek bude zapotřebí k úplnému vyplacení této půjčky? - Slávkine čísla
 Slávka si napsala barevnými fixy čtyři různé přirozená čísla: červené, modré, zelené a žluté. Když červené číslo vydělí modrým, dostane jako neúplný podíl zelené číslo a žluté představuje zbytek po tomto dělení. Když vydělí modré číslo zeleným, vyjde její
Slávka si napsala barevnými fixy čtyři různé přirozená čísla: červené, modré, zelené a žluté. Když červené číslo vydělí modrým, dostane jako neúplný podíl zelené číslo a žluté představuje zbytek po tomto dělení. Když vydělí modré číslo zeleným, vyjde její - Následujících 54921
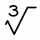 Které z následujících čísel není dokonalá kostka? a. 64 b. 729 c. 800 d. 1331
Které z následujících čísel není dokonalá kostka? a. 64 b. 729 c. 800 d. 1331 - Z5–I–4 MO 2018
 V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně?
V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně? - MO Z8-I-2 2012
 Číslo X je nejmenší takové přirozené číslo, jehož polovina je dělitelná třemi, třetina dělitelná čtyřmi, čtvrtina dělitelná jedenácti a jeho polovina dává zbytek 5 po dělení sedmi. Najděte toto číslo.
Číslo X je nejmenší takové přirozené číslo, jehož polovina je dělitelná třemi, třetina dělitelná čtyřmi, čtvrtina dělitelná jedenácti a jeho polovina dává zbytek 5 po dělení sedmi. Najděte toto číslo.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
