Příklady na trojúhelník - strana 113 z 124
Počet nalezených příkladů: 2480
- Průměr kmene stromu
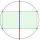Jaký průměr musí mít kmen stromu, aby z něj dal vytesat trám se čtvercovým průřezem o straně 20 cm? - Obsah kruhu opsaného čtverci Vypočítej obsah kruhu, který je popsán čtverce se stranou dlouhou 7,5 cm.
- Dvě tětivy
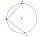Je dána kružnice k (S, r). Z bodu A který patří k jdou dvě tětivy s délkou r. Jaký úhel svírají? Narysuj a odměř. - Úhlopříčky v deltoidu
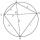Vypočítejte úhlopříčky v deltoidu se stranami 10, 12,6 a 5 cm - Čtyřboký jehlan
Daný je pravidelný čtyřboký jehlan s podstavou čtverec. Výška tělesa je 30 cm a V = 1000cm³. Vypočítejte stranu a a obsah. - Vypočítejte 7
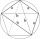Vypočítejte délku úhlopříčky pravidelného pětiúhelníku: a) vepsaného do kružnice o poloměru 12dm; b) opsaného kružnici o poloměru 12dm. - Kruh 3
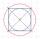Určete obsah kruhu, který je a) vepsán, b) opsán čtverci o straně 6,32 cm. - Tětiva
Jakou délku x má tětiva kružnice o průměru 120 km, pokud je vzdálena od středu kružnice 14 km? - Devítiúhelník
Vypočítej obvod pravidelného devítiúhelníku vepsaného do kružnice s poloměrem 22 cm. - 30-úhelník
V pravidelném 30-ti úhelníku je poloměr kružnice vepsané 15cm. Zjištěte velikost hrany „a", poloměr kružnice opsané „R", obvod a obsah. - Šestiúhelník S
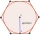Vypočítejte plochu pravidelného šestiúhelníku vepsaného do kruhu s poloměrem r=14 cm. - n-úhelník
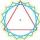Jaká je délka strany pravidelného 8-úhelníku vepsaného do kružnice o poloměru 8 cm? - Je dána 4
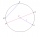Je dána kružnice o poloměru 10 cm a její tětiva, která má délku 12 cm. Vypočtěte velikost středového úhlu, který této tětivě přísluší. - Vypočítej úseč
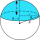Vypočítejte objem kulového úseče a obsah kulového vrchlíku, pokud r = 5 cm (poloměr koule), ρ = 4 cm (poloměr kružnice úseče). - Kružnice a koza
Jaký je poloměr kružnice, která má střed na jiné kružnici a průnik obou kruhů je roven polovině plochy prvé kružnice? Tato úloha je matematickým vyjádřením úlohy ze zemědělství. Sedlák má kruhový pozemek, na kterém se pase koza. Protože sedlák chce, aby j - Konstrukce trojúhelníku ABC
Sestroj trojúhelník ABC pokud c=5cm, b=7cm a a=4cm. Potom vytvoř rovnoběžník, osově souměrný s úsečkou AC a změř velikost druhé úhlopříčky tohoto čtyřúhelníku. - Dve tětivy
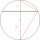Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm. - Konstrukce čtyřúhelníku ABCD
Sestrojte čtyřúhelník ABCD o rozměrech AB, BC, AC, BD a úhlem d = CDA. - Šestihran
Pravidelný šestihran (6 úhelník) se stěnou 6 cm je otočen o 60 ° podél přímky procházející její nejdelší úhlopříčce. Jaký je objem takto vytvořeného tělesa? - Rozměry a objem jehlanu
Pravidelný čtyřboký jehlan je vysoký 2m. Výška boční stěny je 2,8m. Jaké rozměry má podstava? Vypočítej povrch a objem jehlanu.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
