Společná tětiva
Dvě kružnice s poloměry 18 cm a 10 cm se protínají ve dvou bodech. Jejich společná tětiva dlouhá 17 cm. Jaká je vzdálenost středů těchto kružnic?
Správná odpověď:
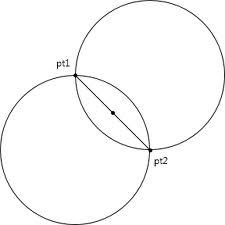
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Vzdálenost 6042
Dvě kružnice s rovnými poloměry 58 mm se protínají ve dvou bodech. Jejich společná tětiva je dlouhá 80 mm. Jaká je vzdálenost středů těchto kružnic? - Vzdálenost 7406
Kružnice s poloměry r1=10 centimetrů a r2=4 cm se zvenčí dotýkají. Jaká je vzdálenost jejich středů? - Vzdálenost 3561
V kružnici o poloměru 10 cm je 12 cm dlouhá tětiva. Vypočítej vzdálenost tětivy od středu kružnice. - Společná tětiva 2
Společná tětiva dvou kružnic k1 a k2 má délku 3,8 cm. Tato tětiva svírá s poloměrem r1 kružnice k1 úhel o velikosti 47°a s poloměrem r2 kružnice k2 úhel 24°30´. Vypočtěte oba poloměry a vzdálenost obou středů kružnic.
- Vypočítejte 83381
Tetiva PQ je dlouhá 10,4 cm a její vzdálenost od středu kruhu je 3,7 cm. Vypočítejte délku druhé tětivy RS, která je 4,1 cm od středu této kružnice. - Průsečíky
Kolik průsečíků budou mít kružnice s poloměry 20 cm a 3 cm, pokud vzdálenost jejich středů je 5 cm. - Tětiva
V kružnici o poloměru r = 70 cm je tětiva 10 × delší než její vzdálenost od středu. Jaká je délka tětivy?
