Úhel - příklady - strana 6 z 60
Počet nalezených příkladů: 1186
- Největší úhel trojúhelníku
Vypočtěte velikost největšího úhlu v trojúhelníku ABC, pokud a = 7 cm, b = 8 cm, c = 13 cm. Vypočítej obsah trojúhelníku, výšku na stranu a. - Výcvik - terč
Plocha pro výcvik střelby má tvar lichoběžníku, jehož rovnoběžné strany jsou dlouhé 36m, 21m, zbývající strany mají délku 14m, 16m. Určete velikost vnitřních úhlů při delší základně. - Souřadnice bodu B
V trojúhelníku ABC určete souřadnice bodu B, pokud víte, že body A, B leží na přímce 3x-y-5=0, body A, C leží na přímce 2x+3y+4=0, bod C leží na souřadnicové ose x a úhel u vrcholu C je pravý. - Koeficient a v rovnici přímky
V rovnici přímky p: ax-2y+1=0 určete koeficient a tak, aby přímka p: a) svírala s kladným směrem osy x úhel 120°, b) procházela bodem A[3,-2], c) byla rovnoběžná s osou x, d) měla směrnici k = 4. - Vzdálenost na globusu
Kolik měří nejkratší vzdálenost po povrchu globusu v měřítku 1:1 000 000 z rovníku na severní pól? - Úhel hodinové ručičky
Na ručičkových hodinách ve třídě projde velká (minutová) ručička na hodinách za nějaký čas úhel 120 stupňů. Jaký úhel za tuto dobu projde malá (hodinová) ručička? - V rovině 2
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel - Užitím
Užitím periodičnosti zjednodušte cos 1125° - Uhly lich
Je dan lichobeznik ABCD a velikosti vnitřních úhlů. Úhel SDC 32° Úhel SAD 33° Úhel SDA 77° Úhel CBS 29°, kde S je průsečnik uhlopříček. Jaká je velikost úhlu BSA? - Středový úhel
Vypočítej středový úhel pokud r = 72 cm a délka oblouku je 12,4 cm. - Lichoběžník všeobecný Ve všeobecném lichoběžníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; |∢VLA| = 70°. Rozděl ho na dva trojúhelníky. Pojmenuj nově vzniklé body. Zapiš délky úseček. Doplň postup konstrukce a sestroj lichoběžník. Postup: 1. VL, |VL| = 5,5cm 2. k1,
- Úhly v trojúhelníku
V jednom trojúhelníku je jeden úhel 43° a druhý je 15° menší než třetí. Určete neznámé úhly trojúhelníku. - V obecném
V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů. - Archeologovia
Archeologové potřebují zjistit velikost nádoby, pokud nalezený střep byl ve tvaru kruhového odstavce o délce 12 cm a výšce 3 cm. Jaký je obsah tohoto odstavce? - Dvě silnice
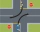Dvě silnice spolu svírají pravý úhel. Na jedné silnici je 5km od křižovatky místo P, na druhé silnici je 12km od křižovatky místo R. Místa P a R jsou spojena přímou pěšinou. Chodec jde z místa R do místa P pěšinou průměrnou rychlostí 5km/h, auto jede z mí - Zakladna a odvěsny Pravoúhlý trojúhelník má zakladnu/odvěsnu/délky 12cm, úhel s přeponou je 13 stupně, jaká je délka druhé přepony?
- Parkování auta
Které parkování pro 5 aut zabírá větší plochu, kolmé nebo šikmé pod úhlem 45° a o kolik. Auto má rozměry 4m a 2m. - Počet vrcholů mnohoúhelníku
V jistém mnohoúhelníku platí, že poměr součtu velikosti jeho vnitřních úhlů a součtu velikosti k nim doplňkových úhlů je 2:5. Kolik vrcholů má tento mnohoúhelník? - V pravoúhlém 9
V pravoúhlém trojúhelníku ABC (pravý úhel při vrcholu C ) je poměr úhlů α : β = 5 : 3. Vypočti velikosti těchto úhlů a převeď je na stupně a minuty (např. 45°20') - Úhly čtyřúhelníku
Ve čtyřúhelníku je úhel α dvakrát větší od úhlu β. úhel γ je 80% úhlu α a úhel δ je o 30° větší od úhlu α. Urč úhly tohoto čtyřúhelníku.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
