Rovnoběžná 81704
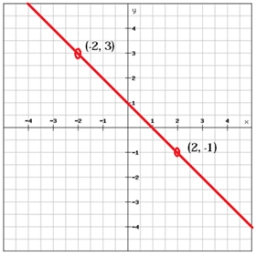
V rovnici přímky p: ax-2y+1=0 určete koeficient a tak, aby přímka p:
a) svírala s kladným směrem osy x úhel 120°,
b) procházela bodem A[3,-2],
c) byla rovnoběžná s osou x,
d) měla směrnici k = 4.
a) svírala s kladným směrem osy x úhel 120°,
b) procházela bodem A[3,-2],
c) byla rovnoběžná s osou x,
d) měla směrnici k = 4.
Správná odpověď:
Tipy na související online kalkulačky
Základem výpočtů v analytické geometrii je dobrá kalkulačka rovnice přímky, která ze souřadnic dvou bodů v rovině vypočítá smernicový, normálový i parametrický tvar přímky, směrnici, směrový úhel, směrový vektor, délku úsečky, průsečíky se souřadnicovým osami atd.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- geometrie
- analytická geometrie
- přímka
- algebra
- rovnice
- vyjádření neznámé ze vzorce
- planimetrie
- trojúhelník
- goniometrie a trigonometrie
- tangens
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Smernicový tvar
Najděte rovnici přímky procházející bodem X [8, 1] a sklonem - směrnicí -2,8. Odpověď zapište ve tvaru y = ax + b, kde a, b jsou konstanty. - Obecná rovnice
Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná - Osová souměrnost
Vypočítejte souřadnice bodu B osově symetricky s bodem A [-1, -3] podél přímky p: x + y - 2 = 0. - Přímka
Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c. - Průsečíkem 82994
Přímka p je dána předpisem y = 1/2 x - 1 . Přímka q je kolmá k přímce p a prochází bodem A [1; 5]. Určete y-ovou souřadnici bodu, který je průsečíkem přímky q s osou y. - Kružnice
Napište rovnici kružnice která procházi bodem [0,6] a dotýka se osy x v bode [5,0]: (x-x_S)²+(y-y_S)²=r² - Dobrý 4
Dobrý den, i když se asi jedná o triviální úlohu nevím si s ní rady. Jde o analytickou geometrii: Najděte všechna celá čísla a, b a c tak, aby přímka zadaná rovnicí ax+by=c procházela body [4,3] a [−2,1]. Děkuji za odpoveď - Přímka 6 Přímka p je dána bodem P [ - 0,5;1] a směrovým vektorem s= (1,5; - 3) určete: A) hodnotu parametru t pro body X [ - 1,5;3], Y [1; - 2] přímky p B) zda body R [0,5; - 1], S [1,5;3] leží na přímce p C) parametrické rovnice přímky m || p, prochází-li přímka
- Koeficienty 59791
Jaká je rovnice přímky, jejíž průsečík x je -3 a průsečík y je -4? Najděte koeficienty A, B, C v rovnici normální čáry: Ax + By = C - Úhel
Daná je přímka p určena rovnicí y = (-8)/(6) x +78. Vypočítejte ve stupních velikost úhlu přímky p s osou y. - Parametricky 6400
Určete úhel přímky, která je určena parametricky x=5+t y=1+3t z=-2t t patři R a roviny, která je určena obecnou rovnicí 2x-y+3z-4=0. - Parametrický tvar
Vypočítejte vzdálenost bodu A[2,1] od přímky p: X=-1+3t Y=5-4t Přímka p má parametrický tvar rovnice přímky. .. - Parabola
Najděte rovnici paraboly, která obsahuje body A[9; 8], B[13; 1], C[16; -10]. (použite y = ax² + bx + c) - Souměrnost
Najděte obraz A´ bodu A[1,2] v osové souměrnosti s osou p: x=-1+3t, y=-2+t (t = jsou realná čísla) - Na přímce
Na přímce p: x=4+t, y=3+2t, t jsou R, určete bod C, který má stejnou vzdálenost od bodů A[1,2] a B[-1,0]. - Určete 47
Určete rovnici kružnice, která prochází bodem M(-1,2) a N( 3,0) a jejíž střed leží na přímce p: x=-3+t, y=-1+t, - Přímky
Najděte hodnotu t, pokud přímky 2tx + 5y-6 = 0 a 5x-4y + 8 = 0 jsou kolmé, rovnoběžné. Jaký úhel svírá každá z přímek s osou x, najděte úhel mezi čarami?
