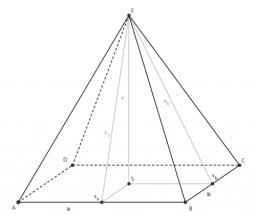
Pyramid
The pyramid has a base rectangle with a = 6cm, b = 8cm. The side edges are the same, and their length is 12.5 cm. Calculate the surface of the pyramid.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- rectangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Rectangular 5798
 The pyramid has a rectangular base with dimensions a = 5cm, b = 6cm. The side edges are identical; their length is h = 11cm. Calculate the surface of the pyramid.
The pyramid has a rectangular base with dimensions a = 5cm, b = 6cm. The side edges are identical; their length is h = 11cm. Calculate the surface of the pyramid. - Quadrilateral 8109
 The regular quadrilateral pyramid has a base diagonal of 5√2 cm, and the side edges are 12√2 cm long. Calculate the height of the pyramid and its surface.
The regular quadrilateral pyramid has a base diagonal of 5√2 cm, and the side edges are 12√2 cm long. Calculate the height of the pyramid and its surface. - The pyramid 4s
 The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of a length of 13 dm. Calculate the surface area and volume of this pyramid.
The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of a length of 13 dm. Calculate the surface area and volume of this pyramid. - Quadrilateral pyramid
 Calculate the surface of a quadrilateral pyramid, which has a rectangular base with dimensions a = 8 cm, b = 6 cm, and height H = 10 cm.
Calculate the surface of a quadrilateral pyramid, which has a rectangular base with dimensions a = 8 cm, b = 6 cm, and height H = 10 cm.
- Pyramid
 Pyramid has a base a = 3cm and height in v = 15 cm. a) calculate the angle between plane ABV and the base plane b) calculate the angle between opposite side edges.
Pyramid has a base a = 3cm and height in v = 15 cm. a) calculate the angle between plane ABV and the base plane b) calculate the angle between opposite side edges. - Quadrilateral pyramid
 Calculate the volume of a quadrilateral pyramid, the base of which has the shape of a rectangle with dimensions a = 6cm, b = 4cm, and height v = 11cm
Calculate the volume of a quadrilateral pyramid, the base of which has the shape of a rectangle with dimensions a = 6cm, b = 4cm, and height v = 11cm - Tetrahedral pyramid
 It is given a regular tetrahedral pyramid with a base edge of 6 cm and a height of pyramid 10 cm. Calculate the length of its side edges.
It is given a regular tetrahedral pyramid with a base edge of 6 cm and a height of pyramid 10 cm. Calculate the length of its side edges. - Quadrilateral 5130
 There is a regular quadrilateral pyramid with the base edge length a = 3 cm and with the length of the side edge h = 8 cm. Please calculate its surface area and volume.
There is a regular quadrilateral pyramid with the base edge length a = 3 cm and with the length of the side edge h = 8 cm. Please calculate its surface area and volume. - Tetrahedral pyramid
 A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area).
A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area).
- Tetrahedral pyramid
 Calculate the surface S and the volume V of a regular tetrahedral pyramid with the base side a = 5 m and a body height of 14 m.
Calculate the surface S and the volume V of a regular tetrahedral pyramid with the base side a = 5 m and a body height of 14 m. - Truncated pyramid
 The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base. - Tetrahedral pyramid
 Calculate the volume and surface area of a regular tetrahedral pyramid, its height is $b cm, and the length of the edges of the base is 6 cm.
Calculate the volume and surface area of a regular tetrahedral pyramid, its height is $b cm, and the length of the edges of the base is 6 cm. - Quadrilateral 36061
 In a regular quadrilateral pyramid, the length of the base edge is a = 8 cm, and the length of the side edge is h = 17 cm. Calculate the surface of the pyramid.
In a regular quadrilateral pyramid, the length of the base edge is a = 8 cm, and the length of the side edge is h = 17 cm. Calculate the surface of the pyramid. - Hexagonal pyramid
 Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
- Quadrangular pyramid
 The regular quadrangular pyramid has a base length of 6 cm and a side edge length of 9 centimeters. Calculate its volume and surface area.
The regular quadrangular pyramid has a base length of 6 cm and a side edge length of 9 centimeters. Calculate its volume and surface area. - Calculate 46151
 A pyramid has a square base with an edge length of 6 cm and a height of 6 cm. Calculate the surface of a pyramid.
A pyramid has a square base with an edge length of 6 cm and a height of 6 cm. Calculate the surface of a pyramid. - Quadrangular pyramid
 Given is a regular quadrangular pyramid with a square base. The body height is 30 cm, and volume V = 1000 cm³. Calculate its side and its surface area.
Given is a regular quadrangular pyramid with a square base. The body height is 30 cm, and volume V = 1000 cm³. Calculate its side and its surface area.
