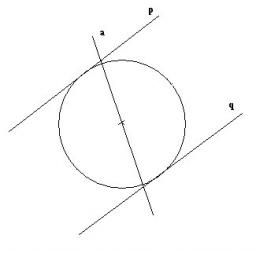
Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q.
Write the equation of the circle and determine the coordinates of the center and radius.
p: x-10 = 0
q: -x-19 = 0
a: 9x-4y+5 = 0
Write the equation of the circle and determine the coordinates of the center and radius.
p: x-10 = 0
q: -x-19 = 0
a: 9x-4y+5 = 0
Correct answer:
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Peter 16
 Peter travels to his uncle's home, 30 km away from his place. He cycles for 2/3 of the journey before the cycle develops a mechanical problem, and he has to push it for the rest of the journey. If he is cycling 10 km per hour faster than his walking speed
Peter travels to his uncle's home, 30 km away from his place. He cycles for 2/3 of the journey before the cycle develops a mechanical problem, and he has to push it for the rest of the journey. If he is cycling 10 km per hour faster than his walking speed - Suppose 10
 Suppose 4+7i is a solution of 5z2+Az+B=0, where A, B∈R. Find A and B.
Suppose 4+7i is a solution of 5z2+Az+B=0, where A, B∈R. Find A and B.
- Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - Increases 80772
 The product of two numbers we know. If we increase the first factor by 2 and decrease the second factor by two, the product increases by 4. How much does the product change if we decrease the first factor by 3 and increase the second factor by 3?
The product of two numbers we know. If we increase the first factor by 2 and decrease the second factor by two, the product increases by 4. How much does the product change if we decrease the first factor by 3 and increase the second factor by 3? - Mountain climbing
 Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x?
Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x? - FX parabola
 Determine the equation of the parabola going through the following co-ordinates (1;2), (-1;-2), and (2;7)
Determine the equation of the parabola going through the following co-ordinates (1;2), (-1;-2), and (2;7) - Find k
 Find k so that the terms k-3, k+1, and 4k-2 form a geometric sequence. Show your solution.
Find k so that the terms k-3, k+1, and 4k-2 form a geometric sequence. Show your solution.
- A speedboat
 A speedboat goes 900 km against a current of 25 km/hr. Its trip took 10 minutes longer than it would have taken to travel with the current. What is the speedboat's speed in still water?
A speedboat goes 900 km against a current of 25 km/hr. Its trip took 10 minutes longer than it would have taken to travel with the current. What is the speedboat's speed in still water? - An integer
 An integer is 17 more than five times another. If the product of the two integers is -6, then find the integers.
An integer is 17 more than five times another. If the product of the two integers is -6, then find the integers. - The same book
 Alexander and Blanka bought the same book that had 240 pages. Blanka read four pages more a day than Alexander. Blanka read it before Alexander. Alexander read the book both weekend days longer. Using an equation or system of equations, calculate how many
Alexander and Blanka bought the same book that had 240 pages. Blanka read four pages more a day than Alexander. Blanka read it before Alexander. Alexander read the book both weekend days longer. Using an equation or system of equations, calculate how many - 11990 perimeter RT
 A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length.
A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length. - The ratio 7
 The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares.
The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares.
- Two simple
 Two simple fractions have the product of 3/10. When the smaller fraction is divided by the bigger fraction, the quotient is 5/6. What are the two fractions in simplest form?
Two simple fractions have the product of 3/10. When the smaller fraction is divided by the bigger fraction, the quotient is 5/6. What are the two fractions in simplest form? - One leg
 One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle.
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle. - Two workers
 One worker makes a part 4 hours and the second 9 hours later than they would make the same part together. How long does it take for each worker to make the part himself?
One worker makes a part 4 hours and the second 9 hours later than they would make the same part together. How long does it take for each worker to make the part himself?
