Pythagorean theorem - math word problems - page 24 of 73
Number of problems found: 1450
- Circle and square
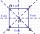 An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Equilateral triangle vs circle
 Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy?
Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy? - Rectangular garden
 The sides of the rectangular garden are in a ratio of 1:2. The diagonal has a length of 20 meters. Calculate the area and perimeter of the garden.
The sides of the rectangular garden are in a ratio of 1:2. The diagonal has a length of 20 meters. Calculate the area and perimeter of the garden. - A truck
 A truck departs from a distribution center. From there, it goes 20km west, 30km north and 10km west and reaches a shop. How can the truck reach back to the distribution center from the shop (what is the shortest path)?
A truck departs from a distribution center. From there, it goes 20km west, 30km north and 10km west and reaches a shop. How can the truck reach back to the distribution center from the shop (what is the shortest path)? - Thunderstorm
 The height of the pole before the storm is 10 m. After a storm, when they check it, they see that the ground from the pole blows part of the column. The distance from the pole is 3 meters. At how high was the pole broken? (In fact, the pole created a rect
The height of the pole before the storm is 10 m. After a storm, when they check it, they see that the ground from the pole blows part of the column. The distance from the pole is 3 meters. At how high was the pole broken? (In fact, the pole created a rect - Pendulum
 Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm.
Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm. - Billboard
 A rectangular billboard is 2.5 m long with a diagonal of 2.8 m long. Calculate the perimeter and the area of the billboard.
A rectangular billboard is 2.5 m long with a diagonal of 2.8 m long. Calculate the perimeter and the area of the billboard. - The rope
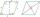 A 68-centimeter-long rope is used to make a rhombus on the ground. The distance between a pair of opposite side corners is 16 centimeters. What is the distance between the other two corners?
A 68-centimeter-long rope is used to make a rhombus on the ground. The distance between a pair of opposite side corners is 16 centimeters. What is the distance between the other two corners? - Carpenter - kitchen
 The carpenter leaned the two-meter kitchen counter against the wall. The lower edge is 0.75m away from the wall. At what height from the ground is the board's top edge resting?
The carpenter leaned the two-meter kitchen counter against the wall. The lower edge is 0.75m away from the wall. At what height from the ground is the board's top edge resting? - The cellar
 Mr. Novák has a cellar, and the cellar window in the chalet is a 0.6-meter square window. The window wishes to place an X-shaped grid in a square. He uses iron welded bars. Calculate the lengths of individual bars and the total length of the bars he has t
Mr. Novák has a cellar, and the cellar window in the chalet is a 0.6-meter square window. The window wishes to place an X-shaped grid in a square. He uses iron welded bars. Calculate the lengths of individual bars and the total length of the bars he has t - Rectangle - parallelogram
 A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle.
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - RT leg and perimeter
 The right triangle ABC with hypotenuse c has the length of a leg a= 84 and the perimeter of the triangle o = 226. Calculate the size of the sides of the triangle ABC.
The right triangle ABC with hypotenuse c has the length of a leg a= 84 and the perimeter of the triangle o = 226. Calculate the size of the sides of the triangle ABC. - Measurements of a triangle
 Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft - Silver medal
 A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part? b) What is the area of the Golden Cross?
A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part? b) What is the area of the Golden Cross? - Rhomboid
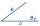 The rhomboid sides' dimensions are a= |AB|=5cm, b = |BC|=6 cm, and the angle's size at vertex A is 60°. What is the length of the diagonal AC?
The rhomboid sides' dimensions are a= |AB|=5cm, b = |BC|=6 cm, and the angle's size at vertex A is 60°. What is the length of the diagonal AC? - ISO trapezoid v2
 The bases of the isosceles trapezoid are measured 20 cm and 4 cm, and their perimeter is 55 cm. What is the area of a trapezoid?
The bases of the isosceles trapezoid are measured 20 cm and 4 cm, and their perimeter is 55 cm. What is the area of a trapezoid? - Road embankment
 Road embankment has a cross-section shape of an isosceles trapezoid with bases 7 m and 10 m and 5 m long leg. How many cubic meters of soil is in an embankment length of 1198 meters?
Road embankment has a cross-section shape of an isosceles trapezoid with bases 7 m and 10 m and 5 m long leg. How many cubic meters of soil is in an embankment length of 1198 meters? - Steps
 How many steps do you save if you go square estate for diagonal (crosswise) rather than circumvent the two sides of its perimeter with 458 steps?
How many steps do you save if you go square estate for diagonal (crosswise) rather than circumvent the two sides of its perimeter with 458 steps? - Square 2
 Points D[10,-8] and B[1,-10] are opposed vertices of the square ABCD. Calculate the area of the square ABCD.
Points D[10,-8] and B[1,-10] are opposed vertices of the square ABCD. Calculate the area of the square ABCD. - Chord
 In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord?
In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
