Pythagorean theorem - math word problems - page 26 of 67
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as:c2 = a2 + b2
where c is the length of the hypotenuse, and a and b are the lengths of the other two sides.
A common proof of the Pythagorean Theorem is called the "area proof". To prove the theorem using this method, we can create a square with side length c and two smaller squares with side lengths a and b, as shown in the figure. We can then place the smaller squares next to each other to form a rectangle with area a x b. We can then see that the area of the square with side length c is equal to the sum of the areas of the smaller squares, which is equal to the area of the rectangle. This demonstrates that c2 = a2 + b2, as stated in the theorem.
Another proof is Euclidean proof which is based on the Euclidean geometry and construction of a line segment that is c and perpendicular to the line segment of a and b.
Number of problems found: 1340
- Circumference 4956
 Calculate the circumference of a diamond whose area is 288cm square and one diagonal is 12.4cm.
Calculate the circumference of a diamond whose area is 288cm square and one diagonal is 12.4cm. - Numerically 4839
 Calculate the diagonal of such a square, for which it holds that its area is equal to its perimeter (without considering units, numerically ...).
Calculate the diagonal of such a square, for which it holds that its area is equal to its perimeter (without considering units, numerically ...). - 2-meter-long 81619
 How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height.
How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height. - Right-angled 81019
 In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
- Horizontal 26131
 What height difference does the 2.5 km long ski lift overcome when the horizontal distance of the entry and exit station is 1200 meters?
What height difference does the 2.5 km long ski lift overcome when the horizontal distance of the entry and exit station is 1200 meters? - Position 19113
 The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po
The column is fixed in a vertical position by 3 ropes, which are caught at the height of 3 m above the ground. The other ends of the ropes are anchored to the ground at a distance of 4 m from the base of the column. How much rope was used to secure the po - Right-angled 5804
 We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters
We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters - Determine 5324
 An isosceles triangle with base c and arms a is given by: a = 50.3 cm c = 48.2 cm Determine the interior angles and heights of the base c.
An isosceles triangle with base c and arms a is given by: a = 50.3 cm c = 48.2 cm Determine the interior angles and heights of the base c. - Centimeters 4162
 Calculate for me the length of the diagonal of a rectangle whose size is 7 cm greater than its width and whose perimeter is 34 centimeters. The dimensions of the rectangle are expressed in natural numbers.
Calculate for me the length of the diagonal of a rectangle whose size is 7 cm greater than its width and whose perimeter is 34 centimeters. The dimensions of the rectangle are expressed in natural numbers.
- Plane II
 A plane flew 50 km on a bearing of 63°20' and then flew in the direction of 153°20' for 140km. Find the distance between the starting point and the ending point.
A plane flew 50 km on a bearing of 63°20' and then flew in the direction of 153°20' for 140km. Find the distance between the starting point and the ending point. - Tiles
 How much will you pay CZK for laying tiles in a square room with a diagonal of 8 m if 1 m² cost CZK 420?
How much will you pay CZK for laying tiles in a square room with a diagonal of 8 m if 1 m² cost CZK 420? - Silver medal
 A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part? b) What is the area of the golden cross?
A circular silver medal with a diameter of 10 cm is an inscribed gold cross consisting of five equal squares. What is the area of the silver part? b) What is the area of the golden cross? - Isosceles trapezoid
 Calculate the area of an isosceles trapezoid whose bases are in the ratio of 4:3; leg b = 13 cm and height = 12 cm.
Calculate the area of an isosceles trapezoid whose bases are in the ratio of 4:3; leg b = 13 cm and height = 12 cm. - Surveyor
 Calculate the area of what may vary rectangular, if it focused by surveyor and found the dimensions 10 x 16 m while in each of the four joint points can be position deviation 8 cm?
Calculate the area of what may vary rectangular, if it focused by surveyor and found the dimensions 10 x 16 m while in each of the four joint points can be position deviation 8 cm?
- River
 From the observatory 11 m high and 24 m from the riverbank, river width appears in the visual angle φ = 13°. Calculate the width of the river.
From the observatory 11 m high and 24 m from the riverbank, river width appears in the visual angle φ = 13°. Calculate the width of the river. - Rhombus
 It is given a rhombus of side length a = 20 cm. Touchpoints of inscribed circle divided his sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
It is given a rhombus of side length a = 20 cm. Touchpoints of inscribed circle divided his sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Right triangle
 Calculate the missing side b and interior angles, perimeter, and area of a right triangle if a=10 cm and hypotenuse c = 16 cm.
Calculate the missing side b and interior angles, perimeter, and area of a right triangle if a=10 cm and hypotenuse c = 16 cm. - Perpendicular 73574
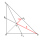 The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line.
The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line. - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
