Angled cyclist turn
The cyclist passes through a curve with a radius of 20 m at 25 km/h. How much angle does it have to bend from the vertical inward to the turn?
Correct answer:
Showing 1 comment:
Matematik
A cyclist has to bend slightly towards the center of the circular track in order to make a safe turn without slipping.
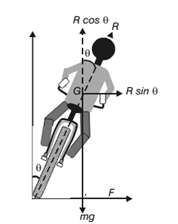
Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:
(i) the component R sin θ, acting towards the center of the curve providing necessary centripetal force for circular motion and
(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
Thus for less bending of the cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner
edge and l be the width of the road then,
Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:
(i) the component R sin θ, acting towards the center of the curve providing necessary centripetal force for circular motion and
(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.
Thus for less bending of the cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner
edge and l be the width of the road then,
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert mass units?
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert mass units?
Do you want to convert velocity (speed) units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- vector
- algebra
- equation
- expression of a variable from the formula
- planimetrics
- right triangle
- triangle
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- My mother
 My mother has 15 grams of gold. How many grams were not used if a pair of earrings need 1 1/4 grams of gold?
My mother has 15 grams of gold. How many grams were not used if a pair of earrings need 1 1/4 grams of gold? - Your chocolate
 Your chocolate chip cookie recipe makes three dozen cookies, but you need four dozen cookies. If the recipe requires 1 7/8 cups of vegetable oil, 2 1/2 teaspoons of almond extract, and 3 1/2 cups of oatmeal, how many of these ingredients are necessary for
Your chocolate chip cookie recipe makes three dozen cookies, but you need four dozen cookies. If the recipe requires 1 7/8 cups of vegetable oil, 2 1/2 teaspoons of almond extract, and 3 1/2 cups of oatmeal, how many of these ingredients are necessary for - Quartile statistics
 Use the following data, which was obtained from a study of weights of adult men, to answer problems: Mean ; 192 lb ; First quartile ; 178lb Median; 185lb ; Third quartile ; 232 lb Mode ; 180 lb ; 86th percentile ; 239 lb Standard Deviation ; 23lb; ; a) Wh
Use the following data, which was obtained from a study of weights of adult men, to answer problems: Mean ; 192 lb ; First quartile ; 178lb Median; 185lb ; Third quartile ; 232 lb Mode ; 180 lb ; 86th percentile ; 239 lb Standard Deviation ; 23lb; ; a) Wh - What power 2
 What power has a pump output to move 4853 hl of water to a height of 31 m for 8 hours? Comparing the power generated by the pump vs. the power generated by the motor, which is more efficient? Which pump or motor generates more pollution if, for every watt
What power has a pump output to move 4853 hl of water to a height of 31 m for 8 hours? Comparing the power generated by the pump vs. the power generated by the motor, which is more efficient? Which pump or motor generates more pollution if, for every watt
- Increases 69454
 The car weighs 1850 kg and increases its speed from 27 to 81 km/h. How much has its kinetic energy increased?
The car weighs 1850 kg and increases its speed from 27 to 81 km/h. How much has its kinetic energy increased? - Pump power
 Determine the pump power if: I pour 3 m³ of water from the tank in 120 seconds with a hose. The height of the hose mouth above the tank is 1.5 m. The water's speed from the hose outlet is 20 m/s.
Determine the pump power if: I pour 3 m³ of water from the tank in 120 seconds with a hose. The height of the hose mouth above the tank is 1.5 m. The water's speed from the hose outlet is 20 m/s. - Newton law
 At what acceleration moves a train with a weight of 800 t start if the traction force of the locomotive is 2 * 105 N?
At what acceleration moves a train with a weight of 800 t start if the traction force of the locomotive is 2 * 105 N? - Two boys
 Two boys weighing 60kg and 90kg move on roller skates and are attracted to each other by a rope. One boy exerts a force of 15N. What force does the other boy exert? What accelerations will the boys gain? Do not consider friction or air resistance.
Two boys weighing 60kg and 90kg move on roller skates and are attracted to each other by a rope. One boy exerts a force of 15N. What force does the other boy exert? What accelerations will the boys gain? Do not consider friction or air resistance. - Tarzan
 Tarzan, weighing m = 90 kg, tries to cross the river by swinging with a vine hanging from a tree leaning over the river. Liana has a length l = 12 m. The speed of the Tarzan in the lowest swing position is v = 8 m/s. Tarzan doesn't know that the liana wil
Tarzan, weighing m = 90 kg, tries to cross the river by swinging with a vine hanging from a tree leaning over the river. Liana has a length l = 12 m. The speed of the Tarzan in the lowest swing position is v = 8 m/s. Tarzan doesn't know that the liana wil
- Free fall 5
 Jeremy accidentally dropped his toy stuffed animal from the balcony of his apartment on the fourth floor. The toy hit the ground at a velocity of 16.0 meters/second. At impact, it took 2.0 seconds for the toy's velocity to reach 0 meters/second. If the to
Jeremy accidentally dropped his toy stuffed animal from the balcony of his apartment on the fourth floor. The toy hit the ground at a velocity of 16.0 meters/second. At impact, it took 2.0 seconds for the toy's velocity to reach 0 meters/second. If the to - Buoyancy force
 An adult male has a volume of about 0.070 m³. How much buoyancy affects him when he is completely immersed in water?
An adult male has a volume of about 0.070 m³. How much buoyancy affects him when he is completely immersed in water? - Chained winch
 When digging a well, a chained winch balances the material. An empty shackle weighs 8 kg, a total of 64 kg. What force must the worker exert on the crank handle when pulling the shackle with a constant movement from a depth of 5 m if the shaft diameter is
When digging a well, a chained winch balances the material. An empty shackle weighs 8 kg, a total of 64 kg. What force must the worker exert on the crank handle when pulling the shackle with a constant movement from a depth of 5 m if the shaft diameter is - Approximately 30131
 Please calculate according to Pascal's law. Calculate the hydrostatic pressure at a depth of 300m below sea level if the density of seawater is approximately 1025kg per m³. At what depth below the surface is the hydrostatic pressure 4.5 MPa?
Please calculate according to Pascal's law. Calculate the hydrostatic pressure at a depth of 300m below sea level if the density of seawater is approximately 1025kg per m³. At what depth below the surface is the hydrostatic pressure 4.5 MPa? - Compressive 19933
 The submarine is at a depth of 50 m below the concave surface of the sea. Find the hydrostatic compressive strength of seawater on a metal cover with an area of 0.6 m².
The submarine is at a depth of 50 m below the concave surface of the sea. Find the hydrostatic compressive strength of seawater on a metal cover with an area of 0.6 m².
- Skid friction
 Find the smallest coefficient of skid friction between the car tires and the road so that the car can drive at a 200 m radius at 108 km/h and does not skid.
Find the smallest coefficient of skid friction between the car tires and the road so that the car can drive at a 200 m radius at 108 km/h and does not skid. - Accelerated motion - mechanics
 The delivery truck, with a total weight of 3.6 t, accelerates from 76km/h to 130km/h in the 0.286 km long way. How much was the force needed to achieve this acceleration?
The delivery truck, with a total weight of 3.6 t, accelerates from 76km/h to 130km/h in the 0.286 km long way. How much was the force needed to achieve this acceleration? - Orlík hydroelectric plant
 The Orlík hydroelectric power plant, built in 1954-1961, consists of four Kaplan turbines. For each of them, the water with a flow rate of Q = 150 m3/s is supplied with a flow rate of h = 70.5 m at full power. a) What is the total installed pow
The Orlík hydroelectric power plant, built in 1954-1961, consists of four Kaplan turbines. For each of them, the water with a flow rate of Q = 150 m3/s is supplied with a flow rate of h = 70.5 m at full power. a) What is the total installed pow
