Distance of points
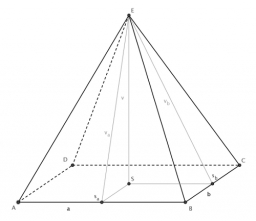
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- similarity of triangles
- algebra
- expression of a variable from the formula
- solid geometry
- pyramid
- space diagonal
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- square
- diagonal
- The Law of Cosines
- goniometry and trigonometry
- cosine
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The angles 5
 The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles.
The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles. - Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - Regular polygons
 The number of sides of two regular polygons differ by 1. The sum of the interior angles of the polygons is in the ratio of 3:2. Calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1. The sum of the interior angles of the polygons is in the ratio of 3:2. Calculate the number of sides of each polygon. - Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
- Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Mast angles and height
 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Using 4
 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
- Three angles
 The three angles of a triangle are (3x-2)°, (4x+5)°, and (2x-3)°, then find the angles.
The three angles of a triangle are (3x-2)°, (4x+5)°, and (2x-3)°, then find the angles. - Know one angle
 In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees. - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - One side 4
 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area.
- A random
 A random sample of 225 nails in a manufacturing company is gathered. The engineer specified that the specified length of a nail must be 8 cm having a standard deviation of 0.04 cm. It shows from the sample that the average length of the nails is 8.055 cm.
A random sample of 225 nails in a manufacturing company is gathered. The engineer specified that the specified length of a nail must be 8 cm having a standard deviation of 0.04 cm. It shows from the sample that the average length of the nails is 8.055 cm. - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
