Geometry - math word problems - page 16 of 162
Number of problems found: 3238
- Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - Two chords
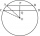 Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords.
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Determine 83003
 Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common.
Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common. - Difference 79094
 Trapezoid, gamma angle=121°, alpha angle=2 thirds of delta angle. Calculate the angle difference alpha, beta
Trapezoid, gamma angle=121°, alpha angle=2 thirds of delta angle. Calculate the angle difference alpha, beta - Triangle ABC
 There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Equation 2604
 The given triangle is ABC: A [-3; -1] B [5; 3] C [1; 5] Write the line equation that passes through the vertex C parallel to the side AB.
The given triangle is ABC: A [-3; -1] B [5; 3] C [1; 5] Write the line equation that passes through the vertex C parallel to the side AB. - Perpendicular projection
 Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0.
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0. - Touch x-axis
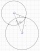 Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis.
Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis. - Equation of circle 2
 Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x.
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x. - Medians in triangle
 The median of the isosceles triangle is 3 cm long. If its perimeter is 16 cm, determine the size of its sides.
The median of the isosceles triangle is 3 cm long. If its perimeter is 16 cm, determine the size of its sides. - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Calculate 6706
 Given a triangle KLM points K [-3.2] L [7, -3] M [8.5]. Calculate the side lengths and perimeter.
Given a triangle KLM points K [-3.2] L [7, -3] M [8.5]. Calculate the side lengths and perimeter. - Circle - AG
 Find the coordinates of the circle and its diameter if its equation is: x² + y² - 6x-4y=36
Find the coordinates of the circle and its diameter if its equation is: x² + y² - 6x-4y=36 - Solutions 45511
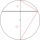 Two parallel chords in a circle with a radius of 6 cm have lengths of 6 cm and 10 cm. Calculate their distance from each other. Find both solutions.
Two parallel chords in a circle with a radius of 6 cm have lengths of 6 cm and 10 cm. Calculate their distance from each other. Find both solutions. - There
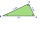 There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a
There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a - Intersections 62784
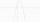 A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3
A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - Coordinates 59863
 The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO
The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO - Quadrilateral PQRS
 PQRS is a quadrilateral with P(4,4), S(8,8), and R(12,8). If vector PQ=4*vector SR, find the coordinates of Q. Solve it
PQRS is a quadrilateral with P(4,4), S(8,8), and R(12,8). If vector PQ=4*vector SR, find the coordinates of Q. Solve it - Chords centers
 The circle has a diameter of 17 cm, upper chord |CD| = 10.2 cm, and bottom chord |EF| = 7.5 cm. The chords H and G midpoints are |EH| = 1/2 |EF| and |CG| = 1/2 |CD|. Find the distance between the G and H if CD II EF (parallel).
The circle has a diameter of 17 cm, upper chord |CD| = 10.2 cm, and bottom chord |EF| = 7.5 cm. The chords H and G midpoints are |EH| = 1/2 |EF| and |CG| = 1/2 |CD|. Find the distance between the G and H if CD II EF (parallel). - Intersections 3
 Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
